2.5 Of 3000
interactiveleap
Sep 21, 2025 · 6 min read
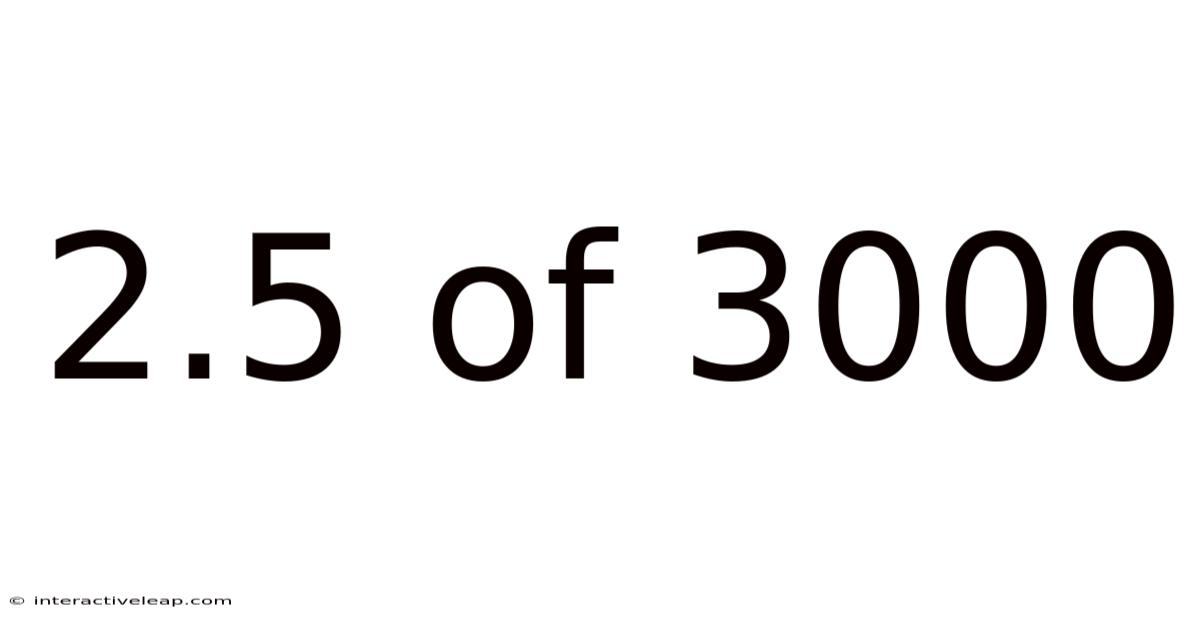
Table of Contents
Understanding the Significance of 2.5 out of 3000: A Deep Dive into Proportions, Percentages, and Context
The seemingly simple fraction "2.5 out of 3000" might appear insignificant at first glance. However, understanding its true meaning requires exploring its proportional representation, converting it to a percentage, and critically examining the context in which it arises. This article will delve into the mathematical interpretations and provide practical examples to illustrate its significance depending on the situation. We will move beyond simple calculation to explore the implications of this fraction in various real-world scenarios. This exploration will enhance your understanding of proportions, percentages, and the importance of context in interpreting numerical data.
Understanding the Basic Calculation
The most straightforward approach is to express "2.5 out of 3000" as a fraction: 2.5/3000. This fraction represents a part of a whole. To simplify, we can multiply both the numerator and denominator by 2 to remove the decimal: 5/6000. Further simplification by dividing both by 5 yields 1/1200. This indicates that 2.5 represents one one-thousand-two-hundredth of the total 3000.
Converting to Percentage
Converting the fraction to a percentage provides a more intuitive understanding. We divide the numerator (2.5) by the denominator (3000) and multiply by 100:
(2.5 / 3000) * 100 = 0.08333...%
This translates to approximately 0.08%. This small percentage highlights the relative insignificance of 2.5 compared to the much larger total of 3000.
Context is King: Interpreting the Significance
The true meaning of "2.5 out of 3000" entirely depends on the context. A seemingly small number can be highly significant in certain situations, while a large number can be insignificant in others. Let's explore some scenarios:
Scenario 1: Environmental Monitoring
Imagine 2.5 out of 3000 water samples tested positive for a harmful pollutant. While the percentage (approximately 0.08%) seems small, it could still represent a concerning environmental issue. This is because even a small contamination rate can have significant long-term consequences for the ecosystem. Further investigation into the source of the pollution becomes crucial.
Scenario 2: Medical Research
Suppose a clinical trial involved 3000 participants, and 2.5 experienced a serious adverse effect from a new drug. Again, the percentage is approximately 0.08%. In this context, this could be alarming. While seemingly a small percentage, it suggests a potential safety concern that requires careful evaluation and possibly modification of the drug or stricter guidelines. The potential long-term health implications for even a small percentage of patients need thorough analysis.
Scenario 3: Manufacturing Defects
Consider a factory producing 3000 units of a product, where 2.5 units are found to be defective. 0.08% might seem acceptable in some industries, especially if the defects are minor. However, in others, even a small defect rate could be unacceptable, especially if the product is safety-critical.
Scenario 4: Academic Performance
If 2.5 out of 3000 students failed a particular exam, the percentage is still approximately 0.08%. This might suggest a very successful teaching approach or perhaps a biased exam that needs re-evaluation. Further investigation into student performance data is necessary to ascertain the reasons behind these results.
Scenario 5: Financial Investments
If an investment portfolio of 3000 assets experienced a loss of 2.5 units, the percentage is still about 0.08%. This could represent a minor fluctuation in a broader portfolio, depending on the value of each asset. The overall profitability of the portfolio must be evaluated rather than focusing solely on the loss percentage.
Exploring the Implications: Beyond the Numbers
Analyzing "2.5 out of 3000" necessitates understanding more than just the simple calculation. Consider these critical points:
-
Magnitude of Impact: The absolute number of incidents (2.5) is important. Even a small percentage can represent substantial losses or risks depending on the context. A small percentage of a large number can still be a significant quantity.
-
Rate of Occurrence: Is this a one-time event, or is it a recurring problem? A single incident might be dismissed, but a consistent recurrence indicates a significant underlying issue.
-
Cost of Correction: What's the cost of addressing the issue? A small percentage might seem insignificant, but if fixing each instance is expensive, the overall cost could be substantial.
-
Statistical Significance: While 0.08% might seem negligible, statistical tests can determine whether this rate is significantly different from expected values. This is especially critical in research studies.
-
Confidence Intervals: When dealing with samples (like in medical trials or surveys), confidence intervals are essential. This indicates the range of values where the true population percentage likely falls, and it considers the sampling error.
Practical Applications and Further Analysis
Understanding proportions and percentages isn't limited to simple calculations. Many sophisticated statistical tools can provide a deeper analysis of data like this. These tools include:
-
Regression Analysis: Used to identify the relationship between variables and predict future outcomes. For example, analyzing the relationship between a specific factor (like weather conditions) and the occurrence of defects in manufacturing.
-
Hypothesis Testing: Used to determine if there is statistically significant evidence to support a hypothesis. For example, testing whether the observed defect rate is significantly higher than the expected rate.
-
Control Charts: Used to monitor processes and detect changes in variability or central tendency. These charts can help identify when a problem emerges and needs attention, even if the percentage is initially small.
Frequently Asked Questions (FAQ)
-
Q: How can I easily convert a fraction like this to a percentage? A: Divide the numerator by the denominator and multiply the result by 100.
-
Q: Is it always necessary to simplify the fraction? A: While simplifying makes it easier to understand, it isn't strictly necessary, particularly if the context requires the original values.
-
Q: How do I determine the statistical significance of a small percentage like this? A: This requires specific statistical tests, like a z-test or t-test, depending on the data and context.
-
Q: What if the number isn't exactly 2.5, but a slightly different value close to it? A: The percentage will be slightly different, but the interpretation in the given context will follow a similar approach.
Conclusion
"2.5 out of 3000" is more than a simple numerical expression. It's a representation of a proportion that requires context-specific analysis. While the percentage is seemingly small (approximately 0.08%), the significance of this value varies widely depending on the situation. Understanding this fraction involves moving beyond the basic calculation and exploring its implications in the broader context. This requires considering factors like the magnitude of impact, the rate of occurrence, the cost of correction, and the use of statistical analysis to determine its true meaning and guide appropriate actions. The key takeaway is that even small percentages can be substantial, depending on their context, and thorough analysis is crucial for informed decision-making.
Latest Posts
Latest Posts
-
Stack Of Pancakes
Sep 21, 2025
-
Mark Henry Leg
Sep 21, 2025
-
33km To Miles
Sep 21, 2025
-
Mg Versus Ml
Sep 21, 2025
-
4th Lateran Council
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 2.5 Of 3000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.