2/3 Of 18
interactiveleap
Sep 24, 2025 · 5 min read
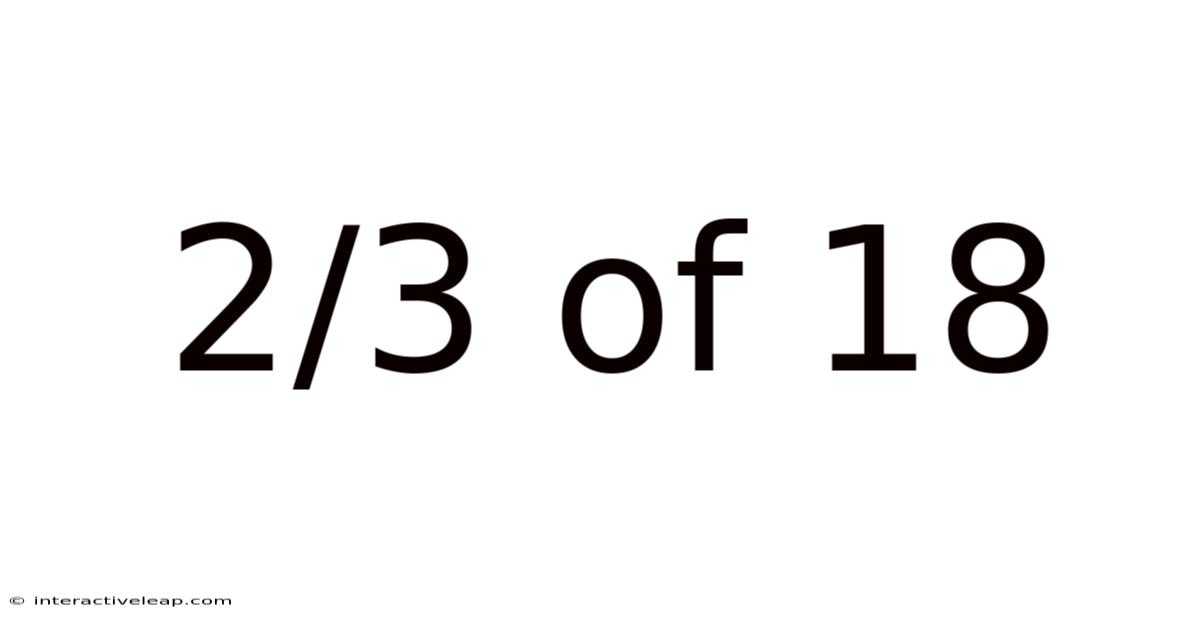
Table of Contents
Decoding 2/3 of 18: A Deep Dive into Fractions and Their Applications
Finding 2/3 of 18 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation opens doors to a broader comprehension of fractions, their practical applications in everyday life, and their importance in more advanced mathematical concepts. This article will explore this seemingly simple problem in depth, unraveling the underlying principles and showcasing its relevance across various fields. We'll move beyond the simple answer and delve into the 'why' behind the calculation, exploring different methods, relatable examples, and addressing frequently asked questions.
Understanding Fractions: The Building Blocks
Before diving into calculating 2/3 of 18, let's establish a firm understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 2/3, 2 is the numerator and 3 is the denominator. This means we're dealing with two parts out of a total of three equal parts.
Visualizing fractions can be incredibly helpful. Imagine a pizza cut into three equal slices. 2/3 of the pizza would represent two of those three slices. This visual representation makes the concept of fractions more concrete and less abstract.
Method 1: Direct Multiplication
The most straightforward method to calculate 2/3 of 18 is through direct multiplication. We can express "of" as multiplication. Therefore, 2/3 of 18 can be written as:
(2/3) * 18
To perform this calculation:
- Multiply the numerator by the whole number: 2 * 18 = 36
- Divide the result by the denominator: 36 / 3 = 12
Therefore, 2/3 of 18 is 12.
Method 2: Finding One-Third and Doubling
An alternative approach involves finding one-third of 18 first, and then doubling the result. This method can be particularly helpful for visualizing the problem and is often easier for beginners to grasp.
- Find one-third: Divide 18 by 3: 18 / 3 = 6. This represents one-third of 18.
- Double the result: Multiply the one-third value by 2: 6 * 2 = 12. This gives us two-thirds of 18.
Again, we arrive at the answer: 2/3 of 18 is 12.
Method 3: Simplifying Before Multiplication (Advanced)
While not strictly necessary for this simple problem, understanding how to simplify fractions before multiplication is crucial for tackling more complex calculations. This involves finding the greatest common divisor (GCD) of the numerator and the denominator, and then dividing both by the GCD.
In this case, we have (2/3) * 18. Notice that 18 can be simplified with the denominator 3. We can rewrite 18 as 3 * 6. Substituting this into our equation, we get:
(2/3) * (3 * 6)
Notice that the 3 in the numerator and the 3 in the denominator cancel each other out. This leaves us with:
2 * 6 = 12
This method showcases a powerful technique for simplifying calculations, especially when dealing with larger numbers or more complex fractions.
Real-World Applications: Where Fractions Matter
Understanding fractions isn't just about solving textbook problems; it's crucial for navigating everyday life. Consider these examples:
- Cooking: A recipe calls for 2/3 cup of sugar. Knowing how to calculate fractions ensures you accurately measure the ingredients.
- Shopping: A store offers a 1/3 off sale. Calculating the discount requires fraction knowledge.
- Construction: Precise measurements in construction rely heavily on fractions and decimals.
- Finance: Understanding percentages (which are essentially fractions expressed as parts of 100) is vital for managing finances, calculating interest, and understanding loan terms.
- Data Analysis: Many statistical and data analysis techniques rely on understanding and manipulating fractions and proportions.
Beyond the Basics: Extending the Concept
The calculation of 2/3 of 18 is a stepping stone to more advanced mathematical concepts. It helps build a foundation for:
- Algebra: Solving algebraic equations often involves working with fractions.
- Calculus: Derivatives and integrals frequently involve manipulating fractions and limits.
- Probability and Statistics: Understanding proportions and ratios, which are closely related to fractions, is essential for analyzing data and calculating probabilities.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Absolutely! Calculators can be used to solve this problem directly by entering (2/3) * 18. However, understanding the underlying principles is crucial for applying the concept in more complex scenarios where a calculator might not be readily available.
Q: What if the question was "What is 18/2 * 3"?
A: This question is mathematically different. The order of operations (PEMDAS/BODMAS) dictates that we perform multiplication and division from left to right. Therefore, 18/2 = 9, and 9 * 3 = 27. This is not the same as finding 2/3 of 18.
Q: How do I explain this concept to a young child?
A: Use visual aids like pizza slices or blocks to represent the fraction. Divide 18 blocks into three equal groups (6 blocks each). Then, take two of these groups (12 blocks) to demonstrate 2/3 of 18.
Q: Are there other ways to express 2/3 of 18?
A: Yes, we can also express the result as a decimal (12.0) or a percentage (100% * 2/3 of 18 = 66.67%). However, the fraction 12 is the most accurate and direct representation for this context.
Conclusion: The Power of Understanding Fractions
Calculating 2/3 of 18, while appearing simple, is a gateway to understanding fundamental mathematical principles. This seemingly basic problem allows us to explore fractions, their practical applications, and their role in more advanced mathematical concepts. By mastering this core concept, we equip ourselves with essential tools for problem-solving in various fields and build a solid foundation for future mathematical endeavors. The journey of understanding this seemingly simple equation highlights the power of breaking down complex concepts into manageable steps, demonstrating that even the simplest problem holds immense educational value. Remember, the true learning lies not just in getting the answer (12), but in comprehending the method and its wider implications.
Latest Posts
Latest Posts
-
15 Of 99
Sep 24, 2025
-
2 7kg In Lb
Sep 24, 2025
-
176lb In Kg
Sep 24, 2025
-
40 Of 80000
Sep 24, 2025
-
104f In C
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.