179 X 2
interactiveleap
Sep 17, 2025 · 5 min read
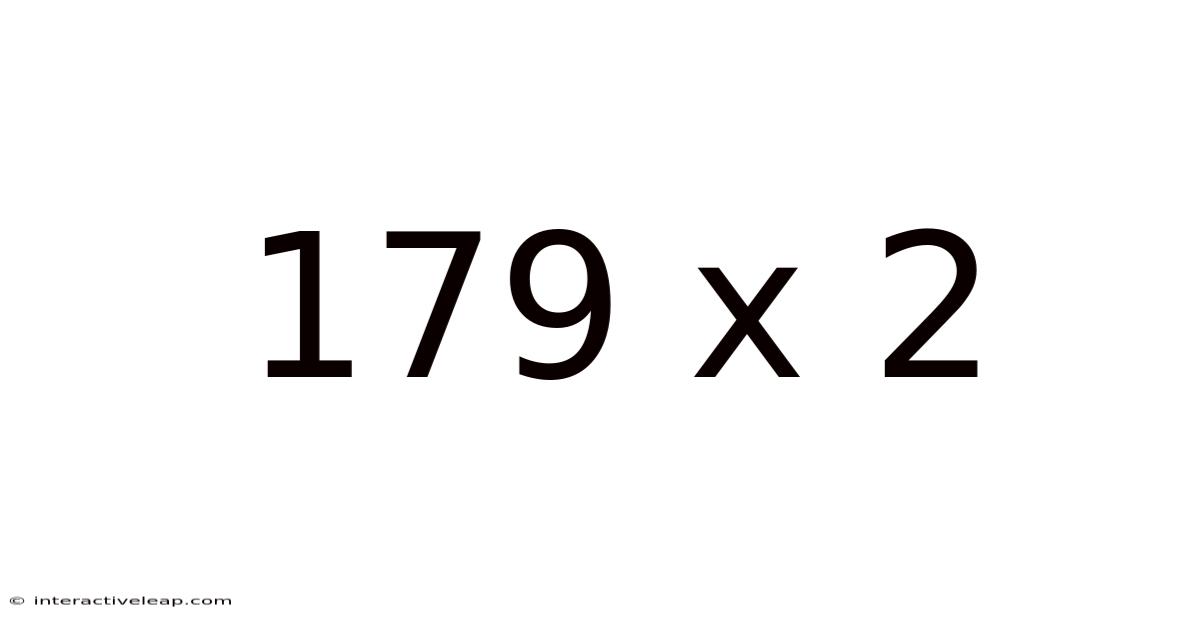
Table of Contents
Unpacking the Simple Calculation: 179 x 2 and the Wonders of Multiplication
This seemingly simple calculation, 179 x 2, serves as a perfect gateway to explore the fundamentals of mathematics, from basic arithmetic to more advanced concepts. While the answer itself is readily obtainable – even with a quick mental calculation for many – delving into the why and how reveals a wealth of knowledge applicable across numerous mathematical disciplines. This article will not only provide the solution but also unpack the underlying principles, explore different methods of calculation, and touch upon the broader implications of this basic multiplication problem.
The Solution and Different Approaches
The answer to 179 x 2 is 358. However, reaching this answer can be achieved through various methods, each offering a unique insight into the nature of multiplication.
1. Traditional Multiplication:
This involves breaking down the multiplication into smaller, manageable steps. We multiply each digit of 179 by 2 individually, starting from the rightmost digit:
- 2 x 9 = 18. Write down '8' and carry-over '1'.
- 2 x 7 = 14. Add the carried-over '1' (14 + 1 = 15). Write down '5' and carry-over '1'.
- 2 x 1 = 2. Add the carried-over '1' (2 + 1 = 3). Write down '3'.
Combining the results gives us 358.
2. Doubling:
This method leverages the concept of doubling. Multiplying by 2 is essentially doubling the number. Therefore, to solve 179 x 2, we simply double 179:
179 + 179 = 358
This method is intuitive and can be easily visualized, making it suitable for beginners and reinforcing the understanding of multiplication as repeated addition.
3. Distributive Property:
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this to our problem by breaking down 179:
179 = 100 + 70 + 9
Therefore, 179 x 2 = (100 + 70 + 9) x 2 = (100 x 2) + (70 x 2) + (9 x 2) = 200 + 140 + 18 = 358
This method is excellent for illustrating the underlying principles of multiplication and its relationship to addition. It highlights how multiplication can be broken down into simpler calculations, making complex problems more manageable.
Beyond the Calculation: Exploring Related Concepts
The seemingly simple calculation of 179 x 2 opens doors to a broader understanding of mathematical concepts.
1. Number Systems:
This calculation can be performed using various number systems, not just the decimal system (base-10) we commonly use. For example, converting 179 and 2 into binary (base-2) and performing the multiplication will still yield the same result (though represented differently). Exploring this further deepens the understanding of number representation and its implications.
2. Algebra:
Imagine the problem as an algebraic equation: 2x = ? where x = 179. Solving for the unknown (x) introduces the concept of inverse operations – in this case, division. Understanding this relationship between multiplication and division is fundamental in algebra.
3. Geometry:
Visualizing multiplication geometrically can provide a different perspective. For instance, we can represent 179 x 2 as the area of a rectangle with sides of length 179 and 2. This connects multiplication to geometric concepts like area and perimeter.
4. Real-World Applications:
The simplicity of 179 x 2 belies its wide-ranging applications in everyday life. From calculating the total cost of two identical items priced at $179 to determining the total distance traveled after covering 179 miles twice, the utility of this seemingly simple calculation is vast.
Expanding the Scope: Working with Larger Numbers
While this article focuses on 179 x 2, the principles discussed are scalable. Understanding the methods used here forms the foundation for tackling more complex multiplication problems, even those involving significantly larger numbers. The same approaches – traditional multiplication, doubling, and the distributive property – can be applied, although the process might become more involved. For instance, multiplying 179 by a larger number such as 12 requires breaking down the multiplication into steps involving multiplying by both 2 (the units digit of 12) and 10 (the tens digit of 12), before finally summing the results.
Furthermore, the use of algorithms and computational tools becomes increasingly relevant when dealing with larger numbers. While mental calculations or manual methods remain valuable for understanding the underlying principles, employing calculators or computer software enhances efficiency and accuracy.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when multiplying?
A: Common errors include: Incorrectly carrying over numbers during traditional multiplication, misplacing digits in the result, and neglecting to account for place value.
Q: Are there any shortcuts for multiplication beyond doubling?
A: Yes, depending on the numbers involved, various shortcuts exist. For example, multiplying by 5 is the same as multiplying by 10 and then dividing by 2. Similarly, multiplying by 25 is the same as multiplying by 100 and dividing by 4.
Q: How can I improve my multiplication skills?
A: Practice is key! Start with simpler problems and gradually increase the complexity. Utilize different methods to understand the underlying concepts. Visual aids and interactive learning tools can also significantly enhance learning.
Q: What is the significance of understanding multiplication beyond just getting the answer?
A: Understanding the fundamental principles of multiplication is crucial for building a strong foundation in mathematics. It lays the groundwork for more advanced concepts in algebra, calculus, and other branches of mathematics and has wide-ranging practical applications in various fields.
Conclusion
The simple calculation of 179 x 2, while appearing trivial at first glance, provides a profound entry point into the world of mathematics. This article has not only provided the answer but also explored different approaches to solving the problem, highlighting the importance of understanding the underlying principles. By delving into related concepts such as number systems, algebra, geometry, and real-world applications, we have demonstrated the far-reaching significance of this seemingly basic calculation. Mastering the principles illustrated here will pave the way for a deeper and more comprehensive understanding of mathematics as a whole, empowering individuals to tackle more complex problems and apply their mathematical knowledge confidently in various contexts. The journey from 179 x 2 to a deeper comprehension of mathematical fundamentals is a testament to the power of learning and exploring the beauty of numbers.
Latest Posts
Latest Posts
-
10 Of 7
Sep 17, 2025
-
80lbs To Stone
Sep 17, 2025
-
50 To Fraction
Sep 17, 2025
-
123 Pounds Kg
Sep 17, 2025
-
6 Of 20000
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 179 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.