17 In Hexadecimal
interactiveleap
Sep 23, 2025 · 6 min read
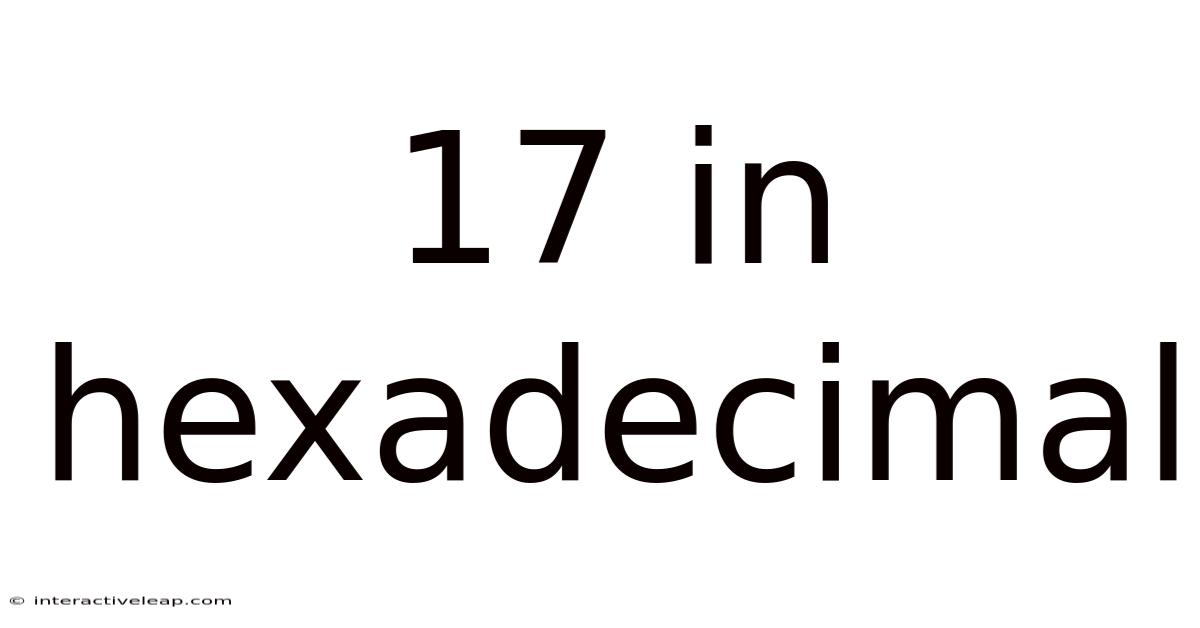
Table of Contents
Decoding 17 in Hexadecimal: A Deep Dive into Number Systems
Have you ever encountered the number 17 in a context that wasn't quite decimal? Perhaps in programming, computer science, or even some specialized technical documentation? If so, you might have stumbled upon its hexadecimal representation. This article will provide a comprehensive exploration of the number 17 in hexadecimal, explaining its conversion, its significance in different contexts, and its broader implications within the world of number systems. We'll cover everything from the basics of hexadecimal to more advanced applications, ensuring a clear and engaging understanding for readers of all technical backgrounds.
Understanding Number Systems
Before diving into the specifics of hexadecimal and the number 17, let's establish a firm understanding of number systems in general. We're most familiar with the decimal system (base-10), which uses ten digits (0-9) to represent numbers. Each place value represents a power of 10. For example, the number 123 is actually (1 x 10²) + (2 x 10¹) + (3 x 10⁰).
Other common number systems include:
- Binary (base-2): Uses only two digits (0 and 1), fundamental to computer science.
- Octal (base-8): Uses eight digits (0-7).
- Hexadecimal (base-16): Uses sixteen digits (0-9 and A-F, where A=10, B=11, C=12, D=13, E=14, and F=15).
Hexadecimal's importance stems from its efficient representation of binary data. Since 16 is a power of 2 (2⁴), each hexadecimal digit can represent four binary digits (bits). This makes hexadecimal a convenient shorthand for representing long binary strings, simplifying readability and reducing potential errors.
Converting Decimal to Hexadecimal
To understand how 17 is represented in hexadecimal, we need to perform a conversion from decimal (base-10) to hexadecimal (base-16). There are two primary methods for this:
Method 1: Repeated Division
This method involves repeatedly dividing the decimal number by 16 and recording the remainders. The remainders, read in reverse order, form the hexadecimal representation.
Let's convert 17 to hexadecimal:
- 17 ÷ 16 = 1 with a remainder of 1
- 1 ÷ 16 = 0 with a remainder of 1
Reading the remainders from bottom to top, we get 11. Therefore, 17 in decimal is 11 in hexadecimal.
Method 2: Place Value System
This method involves finding the largest power of 16 that is less than or equal to the decimal number, and then determining the coefficients for each power of 16.
- The largest power of 16 less than or equal to 17 is 16⁰ (which equals 1).
- 17 can be represented as (1 x 16¹) + (1 x 16⁰).
- This translates to 1 * 16 + 1 * 1 = 17.
- The coefficients 1 and 1 correspond to the hexadecimal digits 1 and 1 respectively, resulting in 11<sub>16</sub>.
Why Hexadecimal is Used in Computing
Hexadecimal's significance in computing arises from its compact representation of binary data. As mentioned earlier, each hexadecimal digit corresponds to four binary digits. This makes it far more concise to represent large binary numbers using hexadecimal. For instance, the binary number 10001 is represented as 11 in hexadecimal, significantly reducing the length and improving readability.
This efficiency is critical in various computing applications:
- Memory Addresses: Hexadecimal is frequently used to represent memory addresses within a computer system. Using hexadecimal simplifies the representation of these addresses, making them easier to read and understand.
- Color Codes: In web design and graphics, hexadecimal is widely used to represent colors using RGB (Red, Green, Blue) values. Each color component is represented by two hexadecimal digits (e.g., #FF0000 represents pure red).
- Data Representation: Hexadecimal is used to display data in many programming environments and debugging tools. Its compact nature makes it easier to interpret raw data, particularly when dealing with large datasets.
- Machine Code: Assembly language, which works directly with machine code instructions, often uses hexadecimal to represent those instructions. This allows programmers to interact more directly with the computer's hardware.
17 in Hexadecimal: Practical Applications
Understanding the representation of 17 (11<sub>16</sub>) provides a stepping stone to comprehending more complex hexadecimal scenarios. Let's explore some practical examples:
- Color Codes (simplified): While not a direct application of 17 itself, understanding hexadecimal representation allows one to interpret color codes. Imagine a simplified color system using only 16 colors. Then,
11could potentially represent a specific color in that system. - Memory Addressing (conceptual): Although memory addresses are generally larger numbers, understanding the basic hexadecimal representation of 17 lays the groundwork for understanding how much larger addresses (e.g., 0x1A2B) are structured.
- Bit manipulation: Understanding hexadecimal allows us to easily translate between binary and a more human-readable format. For instance if we want to set a particular bit in a larger binary number we could use hexadecimal to determine which bit (or combination of bits) to modify.
Frequently Asked Questions (FAQ)
-
Q: Why not use other bases like octal (base-8)? A: While octal is also a power of 2, hexadecimal (base-16) offers a more compact representation of binary data because each hexadecimal digit represents four bits, whereas each octal digit represents only three. This leads to greater efficiency in terms of space and readability.
-
Q: How do I convert a larger decimal number to hexadecimal? A: You can use the repeated division method described above, repeatedly dividing the decimal number by 16 until the quotient is 0. The remainders, read in reverse order, will give you the hexadecimal equivalent.
-
Q: Can I use a calculator to convert between decimal and hexadecimal? A: Yes, many scientific calculators and online converters can perform these conversions easily.
-
Q: Is there a maximum number representable in hexadecimal? A: Theoretically, no. The range of numbers representable depends on the number of digits used. The more digits, the larger the number that can be represented. In practice, computer systems impose limits due to memory constraints.
-
Q: What about negative numbers in hexadecimal? A: Negative numbers are typically handled using two's complement representation, a method that uses the most significant bit (MSB) to indicate the sign.
Conclusion
The number 17, represented as 11 in hexadecimal, serves as a fundamental building block for understanding this crucial number system. Mastering the conversion between decimal and hexadecimal is essential for anyone working with computers, programming, or any field involving digital data. The efficiency and compactness of hexadecimal make it an indispensable tool for representing and manipulating binary data, impacting various aspects of modern computing. By grasping the principles outlined in this article, you'll be well-equipped to navigate the world of hexadecimal numbers and their significant role in the digital realm. From understanding color codes on websites to deciphering low-level programming instructions, a solid grasp of hexadecimal is an invaluable asset in today's technology-driven world. Remember to practice conversions – the more you do, the more intuitive this system becomes.
Latest Posts
Latest Posts
-
91kg In Pounds
Sep 23, 2025
-
26 Times Tables
Sep 23, 2025
-
2500mm In Metres
Sep 23, 2025
-
3 4 1
Sep 23, 2025
-
Disadvantages Gantt Chart
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 17 In Hexadecimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.