15 Of 800
interactiveleap
Sep 15, 2025 · 6 min read
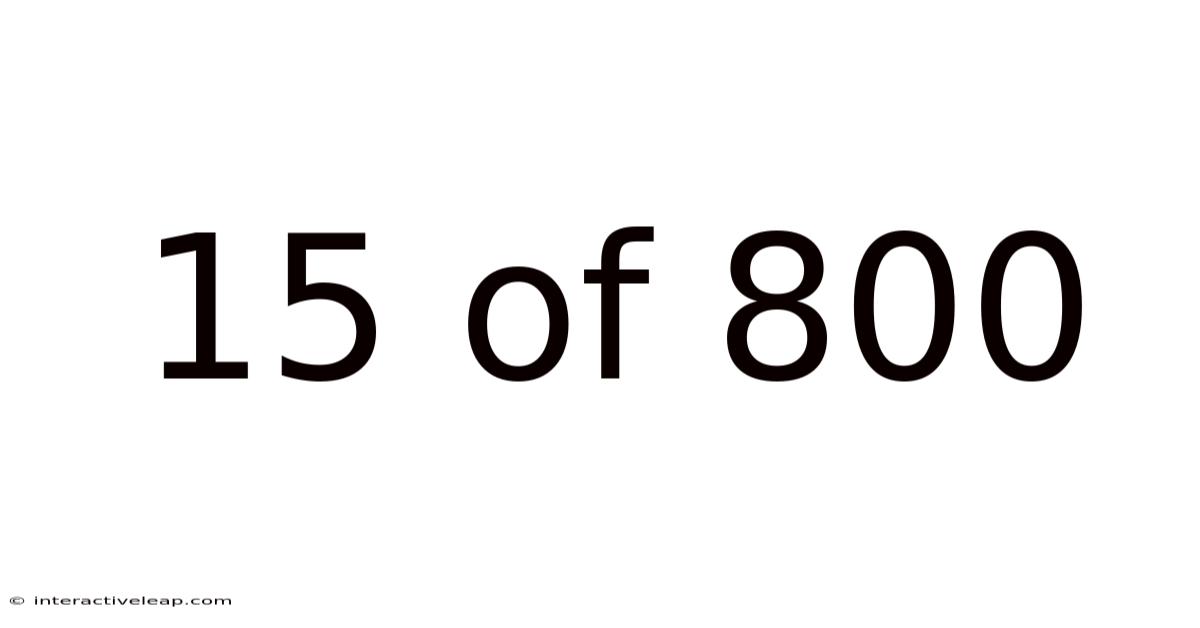
Table of Contents
Unveiling the Mystery: 15 out of 800 – A Deep Dive into Fractions, Percentages, and Ratios
Understanding fractions, percentages, and ratios is fundamental to numeracy. This article delves into the seemingly simple concept of "15 out of 800," exploring its representation in various mathematical forms, practical applications, and the underlying principles that govern these crucial concepts. We'll uncover how to express this fraction in its simplest form, convert it to a percentage, and explore its implications in various real-world scenarios. By the end, you'll not only understand "15 out of 800" but also possess a stronger grasp of fractional, percentage, and ratio calculations.
Understanding Fractions: The Building Blocks
The phrase "15 out of 800" is essentially a fraction. A fraction represents a part of a whole. In this case, 15 represents the part, and 800 represents the whole. We can write this fraction as 15/800.
Key elements of a fraction:
- Numerator: The top number (15) indicating the part.
- Denominator: The bottom number (800) indicating the whole.
Understanding fractions is crucial for various calculations and interpretations. For instance, if 800 represents the total number of students in a school, and 15 represent the number of students who achieved a perfect score on a test, the fraction 15/800 would show the proportion of students who achieved this feat.
Simplifying Fractions: Finding the Essence
The fraction 15/800 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both 15 and 800 without leaving a remainder. In this case, the GCD is 5. Dividing both the numerator and denominator by 5, we simplify the fraction:
15 ÷ 5 = 3 800 ÷ 5 = 160
Therefore, the simplified fraction is 3/160. This simplified fraction retains the same value as 15/800 but is expressed in a more concise and manageable form. Simplifying fractions is essential for clearer understanding and easier calculations.
Converting Fractions to Percentages: A Different Perspective
Percentages provide another way to express a fraction, representing the proportion as a part of 100. To convert 3/160 to a percentage, we perform the following calculation:
(3/160) * 100% = 1.875%
Therefore, "15 out of 800" represents 1.875%. This percentage clearly shows the relatively small proportion that 15 represents compared to the whole (800). Percentages are commonly used to express proportions in various contexts, making them easily understandable and comparable across different datasets.
Ratios: Comparing Quantities
A ratio expresses the relationship between two or more quantities. In the context of "15 out of 800," we can express the ratio of successful outcomes (15) to the total attempts (800) as 15:800. This ratio can be simplified in the same way we simplified the fraction, by dividing both sides by their GCD (5):
15 ÷ 5 : 800 ÷ 5 = 3:160
The ratio 3:160 indicates that for every 3 successful outcomes, there are 160 total attempts. Ratios are useful for comparing quantities, highlighting the proportional relationship between them.
Real-World Applications: Putting it into Practice
The concept of "15 out of 800" and its various representations (fraction, percentage, ratio) have diverse practical applications:
- Statistics: In statistical analysis, this could represent the success rate of a particular event, such as the percentage of students passing an exam (1.875%).
- Quality Control: In manufacturing, it could signify the number of defective items out of a batch of 800, providing insight into product quality.
- Surveys and Polls: If 800 people participated in a survey, and 15 responded positively to a particular question, the fraction, percentage, and ratio help quantify public opinion.
- Finance: This concept can be used in financial calculations, such as determining the return on investment (ROI) or calculating the percentage of successful trades.
- Scientific Research: Experimental data often involves calculating ratios and percentages to analyze results and draw conclusions.
Understanding how to interpret and use these mathematical concepts is essential for accurate data analysis and informed decision-making in a vast range of fields.
Advanced Concepts: Expanding the Understanding
While the basic interpretation and calculations are straightforward, exploring the concept further can enhance understanding:
- Proportions: Understanding proportions allows us to solve problems where one part of a ratio is known, and the other needs to be determined. For example, if we know 3 out of 160 represent a certain percentage, we can calculate the corresponding value for a different total number.
- Probability: The fraction 3/160 can be interpreted as a probability, indicating the likelihood of a specific event occurring (in this case, a probability of 1.875%).
- Statistical Significance: In statistical analysis, determining whether the 1.875% is statistically significant requires further investigation, depending on the context and sample size.
Understanding these advanced concepts provides a deeper appreciation for the mathematical power of representing quantities using fractions, percentages, and ratios.
Frequently Asked Questions (FAQs)
Q1: Can I express 15 out of 800 as a decimal?
A1: Yes, you can. To convert the fraction 3/160 to a decimal, simply divide the numerator by the denominator: 3 ÷ 160 = 0.01875.
Q2: How does the size of the denominator affect the percentage?
A2: A larger denominator means that the same numerator will represent a smaller percentage. For example, 15 out of 100 is 15%, but 15 out of 800 is only 1.875%.
Q3: Are there other ways to simplify 15/800?
A3: While 5 is the greatest common divisor, you could simplify it in steps. For instance, you could divide both by 5 to get 3/160, and then you could use other common divisors if they exist but, in this case, 3 and 160 don’t share common divisors.
Q4: What if I have a different number “out of 800”? How would I perform the calculations?
A4: The process remains the same. Replace the 15 with your new number, then simplify the fraction, convert to a percentage, and express it as a ratio following the same steps outlined above.
Q5: Why is it important to simplify fractions?
A5: Simplifying fractions makes them easier to understand and work with. It also helps to identify relationships and comparisons more easily. A simplified fraction provides a clearer representation of the underlying ratio.
Conclusion: Mastering the Fundamentals
Understanding the concept of "15 out of 800," and its expression as a fraction (3/160), percentage (1.875%), and ratio (3:160), is crucial for anyone looking to enhance their mathematical skills. This seemingly simple concept forms the foundation for more complex mathematical operations and analyses. By mastering these fundamental principles, you equip yourself with the tools for effective interpretation and application in numerous real-world scenarios. The ability to confidently manipulate fractions, percentages, and ratios is a valuable asset across diverse fields, fostering a deeper understanding of data and enhancing your problem-solving capabilities. Remember, consistent practice and a curious mindset are key to solidifying these essential mathematical skills. Keep exploring, keep learning, and you'll continue to unlock the power of numbers!
Latest Posts
Latest Posts
-
95 3kg In Stone
Sep 15, 2025
-
30 Of 110
Sep 15, 2025
-
66 6 To Fraction
Sep 15, 2025
-
Box With X
Sep 15, 2025
-
Squared Cubed Numbers
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 800 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.