15 Of 42000
interactiveleap
Sep 25, 2025 · 6 min read
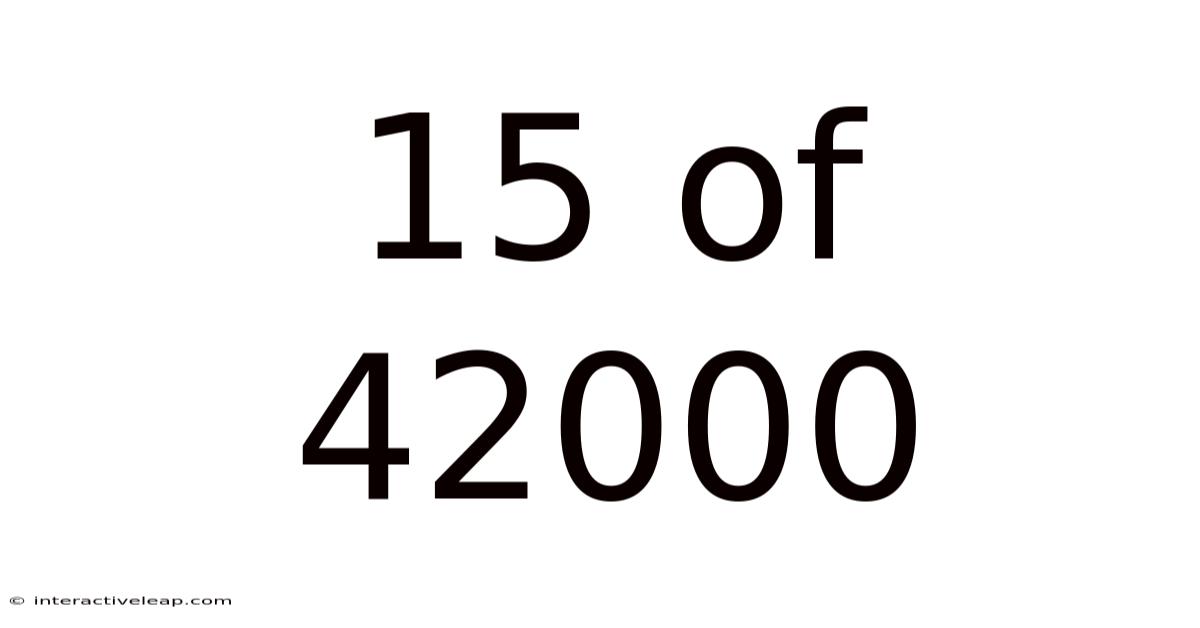
Table of Contents
Decoding 15/42000: Understanding Fraction Reduction and its Real-World Applications
Have you ever encountered a fraction like 15/42000 and wondered how to simplify it? This seemingly complex fraction represents a common challenge in mathematics, particularly in fields involving ratios, proportions, and probability. This article will guide you through the process of reducing 15/42000 to its simplest form, explain the underlying mathematical principles, and illustrate its practical applications in various real-world scenarios. We'll delve into the concepts of greatest common divisor (GCD), prime factorization, and demonstrate how these techniques can be applied to simplify any fraction, no matter how large the numbers.
Understanding Fraction Reduction
Fraction reduction, also known as simplifying fractions, is the process of expressing a fraction in its lowest terms. This means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. A simplified fraction is easier to understand, compare, and use in calculations. The core principle behind fraction reduction relies on the fundamental property of fractions: multiplying or dividing both the numerator and denominator by the same non-zero number doesn't change the fraction's value.
Finding the Greatest Common Divisor (GCD)
The most efficient method for simplifying fractions involves finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both numbers without leaving a remainder. There are several ways to find the GCD:
-
Listing Factors: List all the factors of both the numerator (15) and the denominator (42000). The largest number that appears in both lists is the GCD. While simple for smaller numbers, this method becomes cumbersome for larger numbers like 42000.
-
Prime Factorization: This method involves breaking down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power. This method is more efficient for larger numbers.
-
Euclidean Algorithm: This is an iterative algorithm that repeatedly applies the division algorithm until the remainder is 0. The last non-zero remainder is the GCD. This method is particularly efficient for very large numbers.
Let's apply the prime factorization method to find the GCD of 15 and 42000:
1. Prime Factorization of 15:
15 = 3 x 5
2. Prime Factorization of 42000:
42000 = 42 x 1000 = (2 x 3 x 7) x (2³ x 5³) = 2⁴ x 3 x 5³ x 7
3. Finding the GCD:
Comparing the prime factorizations, we see that the common prime factors are 3 and 5. The lowest power of 3 is 3¹ and the lowest power of 5 is 5¹. Therefore, the GCD of 15 and 42000 is 3 x 5 = 15.
Reducing 15/42000 to its Simplest Form
Now that we've found the GCD (15), we can simplify the fraction:
15/42000 = (15 ÷ 15) / (42000 ÷ 15) = 1/2800
Therefore, the simplified form of 15/42000 is 1/2800.
Explanation of the Mathematical Principles
The process of reducing fractions is based on the equivalence relation in rational numbers. Two fractions, a/b and c/d, are equivalent if and only if ad = bc. This means that if we multiply the numerator and denominator of a fraction by the same non-zero number, we obtain an equivalent fraction. Conversely, if we divide the numerator and denominator by their GCD, we obtain the simplest equivalent fraction. This process preserves the ratio between the numerator and the denominator, representing the same value in a more concise form.
Real-World Applications of Fraction Reduction
Simplifying fractions is not just an abstract mathematical exercise; it has numerous practical applications in various fields:
-
Probability: In probability calculations, fractions often represent the likelihood of an event. Simplifying these fractions makes it easier to understand and compare probabilities. For example, if the probability of an event is 15/42000, simplifying it to 1/2800 gives a clearer picture of how unlikely the event is.
-
Ratios and Proportions: Ratios and proportions are used extensively in various fields, including engineering, finance, and cooking. Simplifying fractions makes it easier to work with ratios and proportions, especially when dealing with large numbers. For instance, if a recipe calls for a ratio of 15 parts flour to 42000 parts water, simplifying the ratio to 1:2800 makes the recipe much more manageable.
-
Data Analysis: When working with data, fractions often represent percentages or proportions. Simplifying fractions makes it easier to interpret and present data in a clear and concise way. For instance, if 15 out of 42000 people in a survey responded positively, simplifying 15/42000 to 1/2800 provides a simplified representation of this data.
-
Engineering and Construction: In engineering and construction, ratios and proportions are crucial for accurate measurements and calculations. Simplifying fractions ensures precision and reduces errors in these fields.
-
Finance and Accounting: Fractions are commonly used in finance and accounting to represent portions of a whole, like shares of a company or portions of a budget. Simplifying these fractions allows for easier comparisons and analysis of financial data.
Frequently Asked Questions (FAQ)
Q: What if the numerator and denominator have no common factors other than 1?
A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form. There's no further simplification possible.
Q: Can I use a calculator to reduce fractions?
A: Many calculators have a fraction function that can automatically simplify fractions. However, understanding the underlying mathematical principles is crucial for developing a strong foundation in mathematics.
Q: Is there a shortcut for finding the GCD for very large numbers?
A: The Euclidean algorithm is a highly efficient algorithm for finding the GCD of large numbers. It's significantly faster than listing factors or prime factorization for very large numbers.
Q: What happens if I divide the numerator and denominator by a number that is not the GCD?
A: You will get a simplified fraction, but it will not be in its simplest form. You will need to continue simplifying until you reach the GCD.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also presents information in a more concise and efficient manner.
Conclusion
Reducing fractions like 15/42000 to their simplest form (1/2800) is a fundamental mathematical skill with far-reaching implications across numerous disciplines. Mastering this skill, through understanding concepts like the GCD and prime factorization, empowers you to tackle complex mathematical problems with ease and efficiency. It's not merely about manipulating numbers; it's about understanding the underlying principles of ratios, proportions, and the representation of quantities, which are essential for clear communication and problem-solving in various real-world contexts. Remember, the ability to simplify fractions isn't just about getting the right answer; it’s about understanding why that answer is correct and how it applies to the wider world.
Latest Posts
Latest Posts
-
84 7kg To Lbs
Sep 25, 2025
-
1 Of 20
Sep 25, 2025
-
50 X 365
Sep 25, 2025
-
Creative In French
Sep 25, 2025
-
10 Of 145
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 42000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.