15 Divided 2
interactiveleap
Sep 17, 2025 · 5 min read
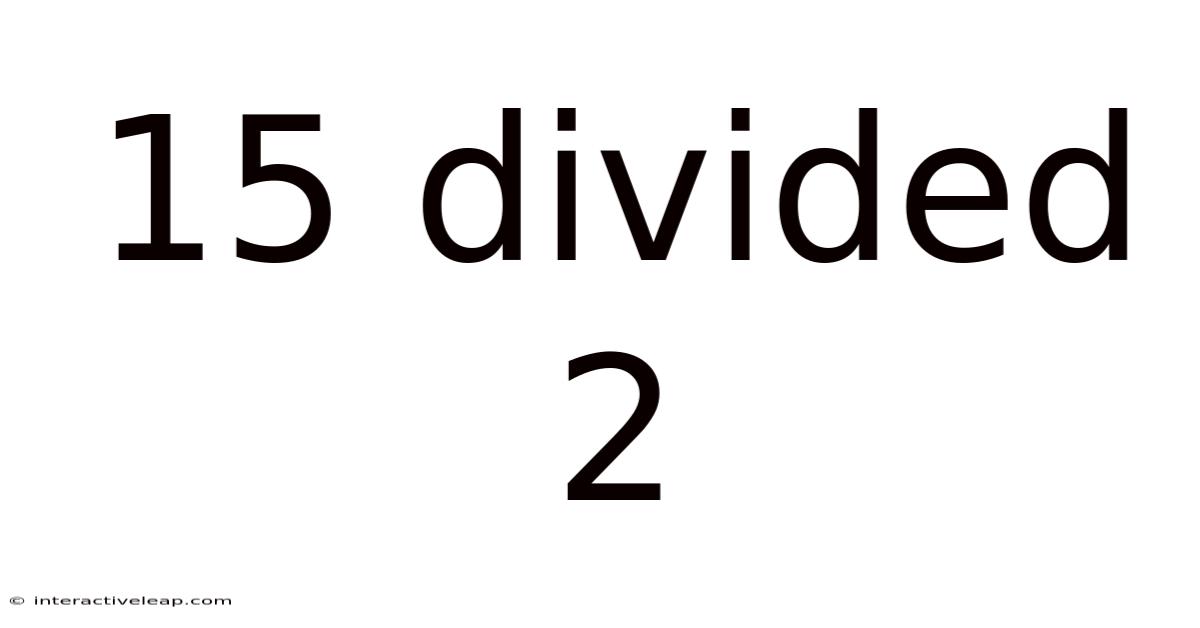
Table of Contents
15 Divided by 2: Unpacking the Basics of Division and Exploring Real-World Applications
Understanding division is a fundamental building block in mathematics, crucial for everything from balancing budgets to designing complex engineering systems. This comprehensive guide delves into the seemingly simple problem of 15 divided by 2, exploring various approaches, explaining the underlying concepts, and highlighting real-world applications. We'll go beyond a simple answer and uncover the richness of this mathematical operation.
Introduction: What Does 15 Divided by 2 Mean?
The expression "15 divided by 2" asks: "How many times does 2 fit into 15?" This simple question opens the door to a deeper understanding of division, encompassing whole numbers, remainders, decimals, and fractions. While a calculator quickly provides the answer, understanding the process behind the answer is far more valuable. This understanding empowers us to solve more complex division problems and to apply the concept in various practical situations.
Calculating 15 Divided by 2: Different Methods
There are several ways to approach 15 divided by 2, each offering a slightly different perspective and highlighting different aspects of the division process.
1. Long Division:
This is a classic method, perfect for building a foundational understanding.
- Set up: Write 15 inside the long division symbol ( ) and 2 outside.
- Divide: 2 goes into 15 seven times (2 x 7 = 14). Write 7 above the 5.
- Multiply: Multiply 2 by 7 (2 x 7 = 14). Write 14 below the 15.
- Subtract: Subtract 14 from 15 (15 - 14 = 1). This is the remainder.
- Result: 15 divided by 2 is 7 with a remainder of 1. This can be written as 7 R1.
2. Repeated Subtraction:
This method emphasizes the concept of division as repeated subtraction.
- Start with 15.
- Subtract 2 repeatedly: 15 - 2 = 13; 13 - 2 = 11; 11 - 2 = 9; 9 - 2 = 7; 7 - 2 = 5; 5 - 2 = 3; 3 - 2 = 1.
- We subtracted 2 seven times before reaching a number less than 2.
- Therefore, 15 divided by 2 is 7 with a remainder of 1.
3. Fractions:
Division can be represented as a fraction. 15 divided by 2 is the same as the fraction 15/2.
- This fraction is an improper fraction because the numerator (15) is larger than the denominator (2).
- We can convert this to a mixed number: Divide 15 by 2 to get 7 with a remainder of 1. The mixed number is 7 1/2.
- This shows that 15 divided by 2 equals 7 and a half.
4. Decimals:
Continuing the fraction approach, we can convert the fraction 15/2 into a decimal.
- Divide 15 by 2 using long division, but instead of stopping at the remainder, add a decimal point and a zero to the remainder (1).
- 2 goes into 10 five times.
- The result is 7.5.
Understanding Remainders and Their Significance
The remainder (1 in this case) represents the portion of 15 that is left over after dividing it into groups of 2. The significance of the remainder depends on the context of the problem.
- Sharing: If you're sharing 15 cookies among 2 people, each person gets 7 cookies, and there's 1 cookie left over.
- Measurement: If you're measuring a 15-meter rope and cutting it into 2-meter lengths, you'll get 7 pieces of 2 meters each, and you'll have 1 meter left.
Ignoring the remainder can lead to inaccuracies or incomplete solutions in many real-world scenarios.
Real-World Applications of Division: Beyond the Classroom
The seemingly simple operation of 15 divided by 2 finds applications in various fields:
- Finance: Calculating equal payments on a loan, splitting bills among friends, or determining the unit cost of an item. For example, if a $15 pizza is split between two people, each pays $7.50.
- Engineering: Designing structures, calculating distances, and distributing resources efficiently. For instance, dividing a 15-meter beam into two equal sections results in two 7.5-meter beams.
- Cooking & Baking: Scaling recipes up or down, dividing ingredients into portions, or calculating baking times. If a recipe calls for 15 grams of sugar for 2 servings, each serving needs 7.5 grams.
- Everyday Life: Sharing resources equally, calculating travel times, determining fuel efficiency, and many more routine tasks. For example, If a journey takes 15 hours and it needs to be divided into two equal shifts, each shift will last 7.5 hours.
- Computer Science: Data processing, algorithm design, and memory allocation all involve division operations. The concept of binary (base-2) in computing relies heavily on division by 2.
Beyond 15 Divided by 2: Expanding Our Understanding
The principles illustrated through 15 divided by 2 apply to all division problems. Understanding the different methods—long division, repeated subtraction, fractions, and decimals—provides a solid foundation for tackling more complex calculations. The ability to interpret remainders and apply the concept to real-world scenarios is crucial for problem-solving in various fields.
Frequently Asked Questions (FAQ)
Q1: What if I need a whole number answer?
A: If the context requires a whole number answer, you would round the result (7.5) to the nearest whole number, either 7 or 8, depending on the specific requirements. The remainder provides the crucial information for making this decision.
Q2: How do I explain 15 divided by 2 to a young child?
A: Use visual aids like objects (15 toys) and divide them into two equal groups. This helps children grasp the concept of sharing equally and understand the remainder as what's left over.
Q3: Can I use a calculator for 15 divided by 2?
A: Yes, a calculator provides a quick answer. However, understanding the underlying process remains essential for problem-solving and developing mathematical intuition.
Conclusion: The Power of Understanding Division
While the answer to 15 divided by 2 might seem straightforward—7.5 or 7 with a remainder of 1—the underlying concepts and applications extend far beyond this simple calculation. Mastering division not only improves mathematical skills but also enhances problem-solving abilities across various disciplines and real-world situations. The seemingly simple act of dividing 15 by 2 opens doors to a richer understanding of mathematics and its practical significance in our lives. Remember, the goal is not just to find the answer but to comprehend the process and its implications. This deeper understanding equips you to confidently tackle more complex mathematical challenges and apply your knowledge to solve problems effectively in various fields.
Latest Posts
Latest Posts
-
Sudan Iii Test
Sep 17, 2025
-
38 4celsius To Fahrenheit
Sep 17, 2025
-
Electronic Variable Orifice
Sep 17, 2025
-
47 Pounds Kg
Sep 17, 2025
-
68 95kg In Stone
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 15 Divided 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.