125 X 12
interactiveleap
Sep 21, 2025 · 6 min read
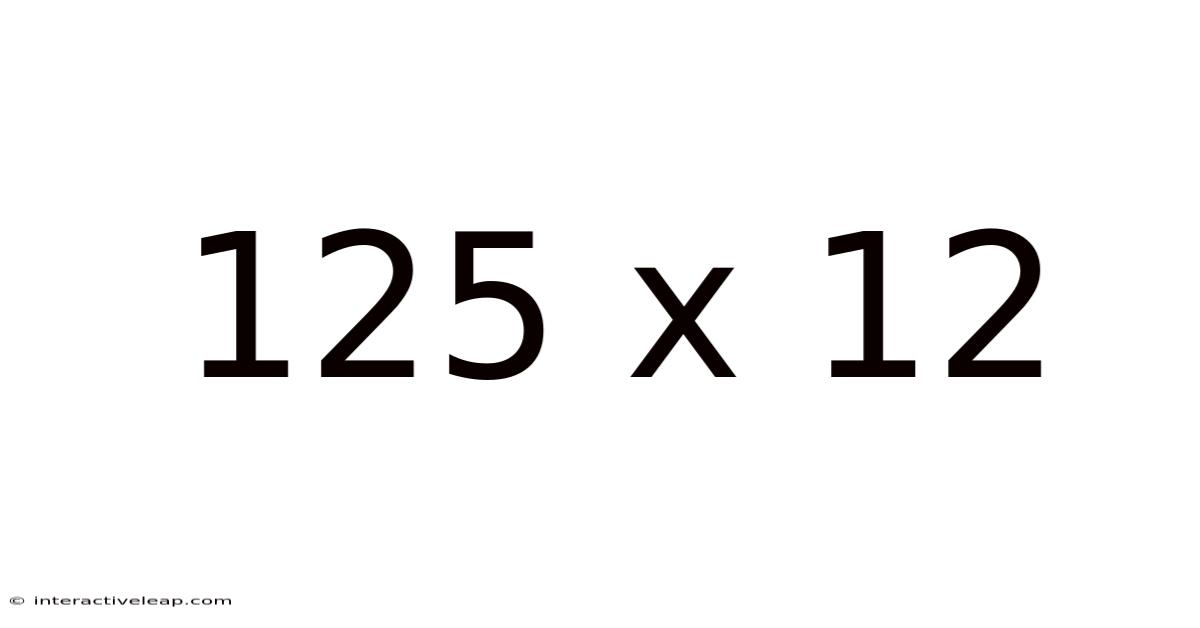
Table of Contents
Decoding 125 x 12: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 125 x 12, delving beyond the immediate answer to uncover the underlying mathematical concepts, practical applications, and various methods for solving it. We'll examine different approaches, from traditional methods to mental math techniques, highlighting the importance of understanding the principles behind multiplication rather than just memorizing results. This will provide a solid foundation for more complex mathematical operations and real-world problem-solving. Understanding multiplication like 125 x 12 is fundamental to success in mathematics and beyond.
Understanding the Basics: What is Multiplication?
Multiplication is a fundamental arithmetic operation that represents repeated addition. When we say 125 x 12, we're essentially asking, "What is the sum of twelve 125s?" This seemingly straightforward concept forms the bedrock of numerous mathematical processes and is crucial for understanding more advanced topics like algebra, calculus, and even programming.
Think of it this way: imagine you have 12 bags, each containing 125 marbles. To find the total number of marbles, you could add 125 twelve times: 125 + 125 + 125 + ... + 125. This is tedious! Multiplication provides a much more efficient way to calculate this: 125 x 12.
Traditional Methods: Solving 125 x 12
Several methods can be used to solve 125 x 12. Let's explore some of the most common:
1. The Standard Algorithm (Long Multiplication)
This is the method most of us learn in elementary school. It involves breaking down the multiplication into smaller steps, multiplying by each digit of the second number separately, and then adding the partial products.
125
x 12
-------
250 (125 x 2)
1250 (125 x 10)
-------
1500 (Sum of partial products)
This method systematically breaks down the problem, making it easier to manage, especially with larger numbers.
2. Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this to solve 125 x 12 by breaking down 12 into 10 + 2:
125 x 12 = 125 x (10 + 2) = (125 x 10) + (125 x 2) = 1250 + 250 = 1500
This method emphasizes the underlying mathematical principles and can be helpful in understanding the logic behind multiplication.
3. Lattice Multiplication
Lattice multiplication, an ancient method, uses a grid to organize the multiplication process. While less common now, it can be a visually appealing and effective technique, particularly for larger numbers.
This method involves creating a grid with rows and columns representing the digits of each number. The individual products are written within the grid, and the diagonals are summed to obtain the final result. (A visual example would be beneficial here but cannot be rendered in this text-based format). Look up "lattice multiplication" online for clear visual instructions.
Mental Math Techniques: Calculating 125 x 12 Quickly
While the standard algorithm is reliable, developing mental math skills can significantly improve calculation speed and efficiency. Here are some techniques for solving 125 x 12 mentally:
1. Utilizing Number Properties
Notice that 125 is one-eighth of 1000. We can leverage this fact:
125 x 12 = (1000/8) x 12 = (1000 x 12) / 8 = 12000 / 8 = 1500
This method requires familiarity with fractions and division but offers a concise solution.
2. Breaking Down the Numbers
We can break down both numbers into simpler components:
125 x 12 = 125 x (10 + 2) = (125 x 10) + (125 x 2) = 1250 + 250 = 1500
This is essentially the distributive property applied mentally.
3. Using Doubles and Halves
This technique involves doubling one number and halving the other to simplify the calculation. While not directly applicable to 125 x 12 in a straightforward manner, it is a useful mental math strategy for other multiplication problems.
Real-World Applications: Where You'll Use 125 x 12
The seemingly simple problem of 125 x 12 has numerous real-world applications:
-
Calculating costs: Imagine you're buying 12 items costing $125 each. The total cost is 125 x 12 = $1500.
-
Area calculations: If you have a rectangular area measuring 125 units by 12 units, its total area is 125 x 12 = 1500 square units.
-
Inventory management: If a warehouse has 12 shelves, each holding 125 boxes, the total number of boxes is 125 x 12 = 1500.
-
Project planning: If a project requires 12 steps, each taking 125 hours, the total time is 125 x 12 = 1500 hours.
These examples highlight how even basic multiplication problems like 125 x 12 are crucial for managing everyday tasks and solving practical problems.
Mathematical Extensions: Building Upon the Fundamentals
Understanding 125 x 12 is not just about getting the answer; it’s about grasping the principles of multiplication and its relationship to other mathematical concepts. This foundation is essential for:
-
Algebra: Solving equations and expressions frequently involves multiplication and the distributive property.
-
Geometry: Calculating areas, volumes, and other geometric properties heavily relies on multiplication.
-
Calculus: Derivatives and integrals involve numerous multiplications and manipulations of algebraic expressions.
-
Data Analysis: Statistical calculations frequently use multiplication in their formulas.
-
Computer Science: Programming algorithms utilize multiplication for various operations, such as array indexing and matrix computations.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to solve 125 x 12?
A: The easiest way depends on your individual preferences and skillset. The standard algorithm is reliable for most, while mental math techniques might be faster for those comfortable with them. The distributive property offers a clear understanding of the underlying mathematical principles.
Q: Are there other methods besides those mentioned to solve this multiplication problem?
A: Yes, there are other less common methods, like using a calculator (which is efficient but doesn't promote understanding) and various abacus methods. The key is to understand the fundamental principles rather than simply relying on a single technique.
Q: Why is it important to understand multiplication beyond just getting the answer?
A: Understanding the principles behind multiplication is crucial for building a strong foundation in mathematics, leading to success in more advanced mathematical concepts and their practical applications in various fields.
Conclusion: Mastering Multiplication for a Brighter Future
This comprehensive exploration of 125 x 12 goes beyond a simple calculation. We've unpacked the underlying mathematical concepts, explored different solution methods, highlighted the importance of mental math, and demonstrated the broad applications of this seemingly basic problem in everyday life and advanced studies. Mastering multiplication, and understanding the ‘why’ behind it, is a significant step towards enhancing mathematical proficiency and problem-solving skills, empowering you to tackle more complex challenges with confidence and competence. Remember, the journey of mathematical understanding is a continuous process of exploration, practice, and application. Embrace the challenges, and you'll be rewarded with a deeper appreciation for the beauty and power of mathematics.
Latest Posts
Latest Posts
-
Ohshc Season 2
Sep 21, 2025
-
101 2f To C
Sep 21, 2025
-
9 24 Simplified
Sep 21, 2025
-
Bell In Oxford
Sep 21, 2025
-
10 Of 1100
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 125 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.