12 Of 600
interactiveleap
Sep 19, 2025 · 5 min read
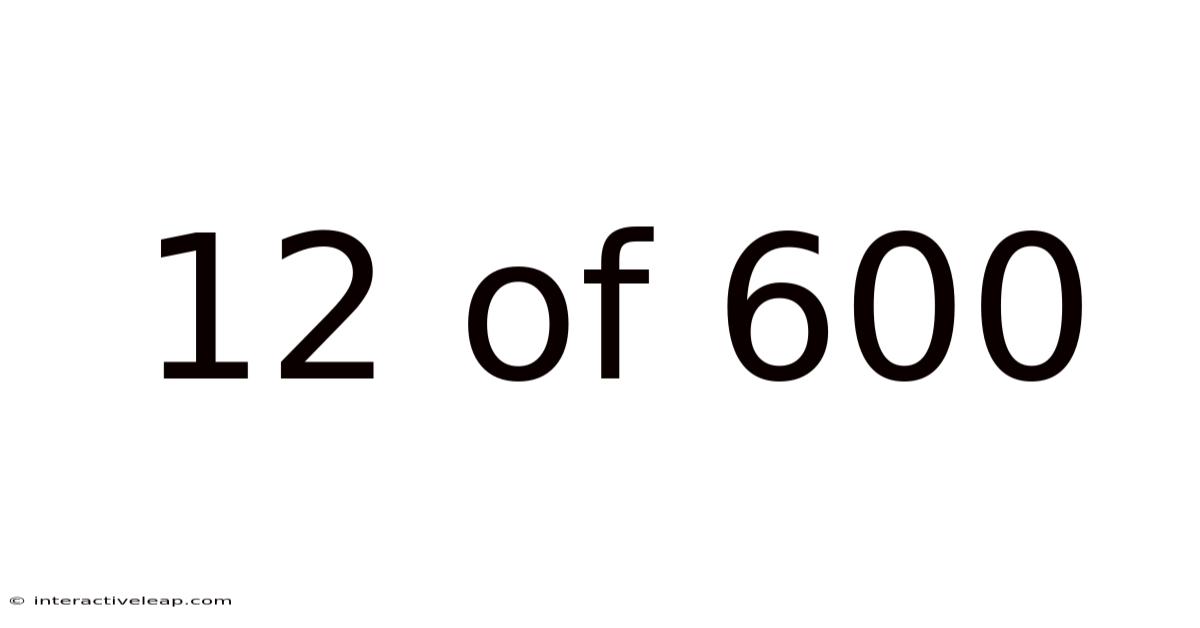
Table of Contents
Unveiling the Mystery: Understanding the Fraction 12/600 and its Implications
The seemingly simple fraction 12/600 might appear insignificant at first glance. However, understanding this fraction, simplifying it, and exploring its applications reveals a wealth of mathematical concepts and practical implications, valuable not just for students but for anyone dealing with proportions, ratios, and percentages in everyday life. This article will delve into the various aspects of 12/600, from basic simplification to its representation in percentage and decimal form, highlighting its uses in different contexts. We’ll also explore related concepts to build a solid understanding of fractions and their significance.
Simplifying 12/600: Finding the Lowest Terms
The first step in understanding any fraction is to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator (12) and the denominator (600) and dividing both by it. Let's break this down:
-
Finding the GCD: The GCD of 12 and 600 can be found using several methods, including prime factorization. The prime factorization of 12 is 2 x 2 x 3 (2² x 3). The prime factorization of 600 is 2 x 2 x 2 x 3 x 5 x 5 (2³ x 3 x 5²). The common factors are 2 x 2 x 3, which equals 12.
-
Simplifying the Fraction: Dividing both the numerator and the denominator by the GCD (12), we get:
12 ÷ 12 / 600 ÷ 12 = 1/50
Therefore, the simplified form of 12/600 is 1/50. This simplified form is much easier to work with and represents the same proportion.
Representing 12/600 as a Decimal and Percentage
Understanding fractions involves being able to convert them into other forms, such as decimals and percentages. This is crucial for various applications, from financial calculations to scientific measurements.
-
Converting to a Decimal: To convert 1/50 (the simplified fraction) to a decimal, we simply divide the numerator (1) by the denominator (50):
1 ÷ 50 = 0.02
Therefore, 12/600 is equivalent to 0.02 as a decimal.
-
Converting to a Percentage: To convert a decimal to a percentage, we multiply by 100:
0.02 x 100 = 2%
Thus, 12/600 represents 2%. This percentage representation is highly useful for understanding proportions and making comparisons.
Real-World Applications of 12/600 (or 1/50 and 2%)
The fraction 12/600, and its simplified equivalent 1/50, appears in numerous real-world scenarios:
-
Percentage Calculations: Imagine a survey where 12 out of 600 respondents answered "yes" to a particular question. This translates to 2%, providing a concise way to summarize the survey results.
-
Proportions in Recipes: If a recipe calls for 12 grams of an ingredient in a 600-gram dish, this simplifies to 1/50, meaning the ingredient represents 2% of the total weight.
-
Financial Analysis: If a company invests $12 out of a total investment of $600 in a specific project, that represents 2% of their total investment portfolio.
-
Probability and Statistics: If an event has a 1/50 chance of occurring, this can be expressed as 2% probability.
Understanding Related Concepts: Fractions, Ratios, and Percentages
To fully grasp the significance of 12/600, it's essential to understand the broader mathematical concepts related to it:
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of parts, while the numerator shows how many parts are being considered.
-
Ratios: A ratio is a comparison between two quantities. It can be expressed as a fraction, using a colon (e.g., 12:600), or with the word "to" (e.g., 12 to 600). The ratio 12:600 is equivalent to the fraction 12/600.
-
Percentages: A percentage is a fraction expressed as a part of 100. It's commonly used to represent proportions and rates. For example, 2% means 2 out of 100, or 2/100. Converting fractions to percentages provides a standardized way to compare proportions.
Expanding the Understanding: Working with Larger Fractions
While 12/600 is a relatively straightforward fraction, understanding its simplification and conversion helps build the foundation for working with more complex fractions. The same principles apply to larger numbers:
-
Finding the GCD: Finding the greatest common divisor remains the crucial first step in simplifying any fraction, no matter the size of the numerator and denominator. Methods like prime factorization or the Euclidean algorithm are essential tools for this.
-
Simplifying to Lowest Terms: Simplifying to lowest terms makes fractions easier to understand and use in calculations. This process ensures the fraction represents the simplest possible proportion.
-
Converting to Decimals and Percentages: The ability to convert fractions to decimals and percentages remains crucial for applying fractions in real-world situations.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 12/600?
A1: The simplest form of 12/600 is 1/50.
Q2: How do I convert 12/600 to a percentage?
A2: First, simplify 12/600 to 1/50. Then, divide 1 by 50 (0.02) and multiply by 100 to get 2%.
Q3: Are ratios and fractions the same thing?
A3: Ratios and fractions are closely related. A ratio compares two quantities, and it can be expressed as a fraction.
Q4: What is the importance of simplifying fractions?
A4: Simplifying fractions makes them easier to understand, compare, and use in calculations. It represents the same proportion in its most concise form.
Q5: Can I use a calculator to simplify fractions?
A5: Many calculators have a function to simplify fractions, although understanding the process manually is valuable for building mathematical skills.
Conclusion: The Significance of 12/600 and Beyond
The seemingly simple fraction 12/600 offers a rich opportunity to explore fundamental mathematical concepts, including simplification, decimal and percentage conversions, and the relationships between fractions, ratios, and percentages. By understanding these concepts, we can apply them to various real-world situations, from analyzing data and solving problems to making informed decisions in various contexts. This exploration underscores the importance of mastering basic arithmetic skills, which serve as a cornerstone for more advanced mathematical understanding and application. The journey from 12/600 to its simplified form, 1/50, and its equivalent decimal (0.02) and percentage (2%), demonstrates the power of simplifying complex information into manageable and easily understandable formats. This ability is crucial not only in mathematics but also across diverse fields, highlighting the practicality and value of seemingly simple mathematical concepts.
Latest Posts
Latest Posts
-
83 Times Table
Sep 19, 2025
-
5 Of 5million
Sep 19, 2025
-
85 Of 70
Sep 19, 2025
-
81 65kg In Stone
Sep 19, 2025
-
Cl To Liters
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 12 Of 600 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.