12 Of 400
interactiveleap
Sep 20, 2025 · 5 min read
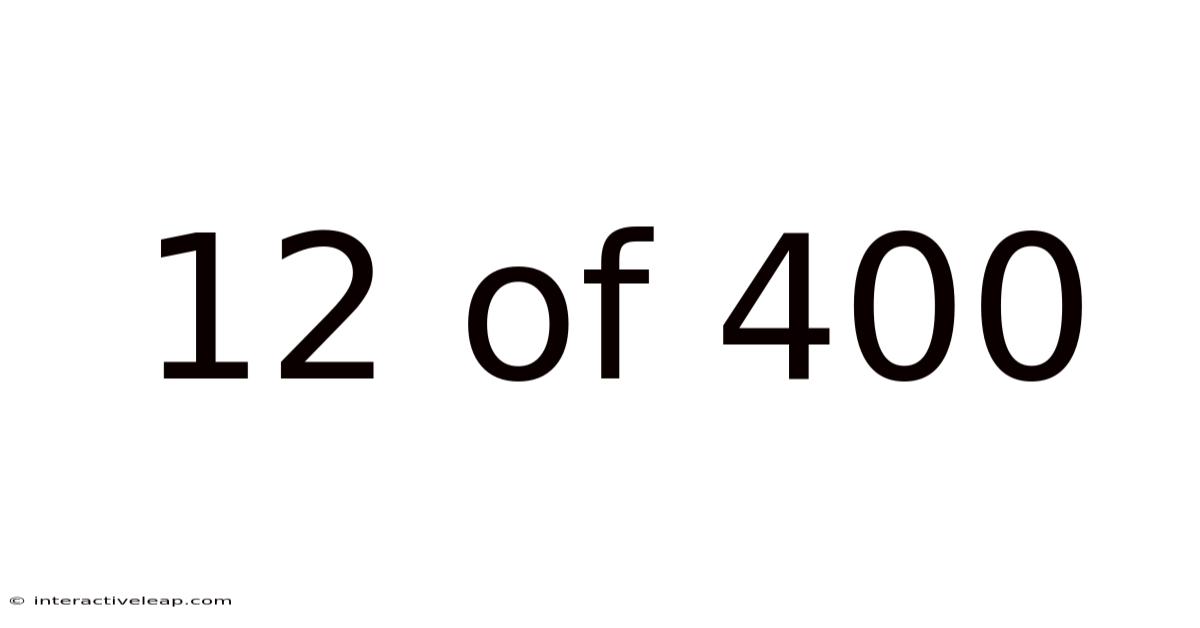
Table of Contents
Decoding the Mystery: Understanding the Fraction 12/400 and its Applications
The seemingly simple fraction 12/400 might appear insignificant at first glance. However, understanding this fraction and its various representations unlocks a deeper understanding of mathematical concepts like simplification, percentages, decimals, and their practical applications in everyday life. This article will delve into the intricacies of 12/400, exploring its simplification, decimal equivalent, percentage representation, and real-world examples. We will also address common questions and misconceptions surrounding fractions like this.
Introduction: The Significance of Fractions
Fractions are fundamental building blocks in mathematics, representing parts of a whole. They are used extensively across various disciplines, from basic arithmetic to advanced calculus, and find practical applications in everyday scenarios like cooking, measuring, and financial calculations. Understanding fractions, especially their simplification and conversion into other forms like decimals and percentages, is crucial for effective problem-solving and data interpretation.
Simplifying 12/400: Finding the Greatest Common Divisor (GCD)
The fraction 12/400 can be simplified by finding the greatest common divisor (GCD) of the numerator (12) and the denominator (400). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
To find the GCD of 12 and 400, we can use the prime factorization method:
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 400: 2 x 2 x 2 x 2 x 5 x 5 = 2⁴ x 5²
The common factors are 2 x 2 = 4. Therefore, the GCD of 12 and 400 is 4.
To simplify the fraction, we divide both the numerator and denominator by the GCD:
12 ÷ 4 / 400 ÷ 4 = 3/100
Therefore, the simplified form of 12/400 is 3/100. This simplified fraction is much easier to work with and provides a clearer representation of the value.
Converting 3/100 to a Decimal: Understanding Decimal Representation
Converting a fraction to a decimal is a straightforward process. In this case, we have the fraction 3/100. Since the denominator is a power of 10 (10² = 100), the conversion is particularly easy. We simply place the numerator (3) and move the decimal point two places to the left:
3/100 = 0.03
This means that 12/400 is equivalent to 0.03. This decimal representation is useful for calculations involving other decimal numbers.
Expressing 3/100 as a Percentage: The Percentage Equivalent
Percentages are widely used to express proportions and ratios. To convert a fraction to a percentage, we multiply the fraction by 100%:
(3/100) x 100% = 3%
This indicates that 12/400 represents 3% of a whole. This percentage representation is particularly helpful for comparisons and data visualizations.
Real-World Applications of 12/400 (or 3/100 or 3%): Practical Examples
The fraction 12/400, and its simplified forms, find applications in various real-world scenarios. Here are a few examples:
-
Surveys and Statistics: Imagine a survey of 400 people where 12 responded positively to a particular question. The fraction 12/400 (or 3%) represents the proportion of positive responses. This data could be used to analyze public opinion or market research.
-
Financial Calculations: If you invested $400 and earned a profit of $12, your return on investment would be 12/400, or 3%. This is a common way to express investment returns.
-
Discounts and Sales: A store might offer a 3% discount on all items. This is equivalent to a discount of 12/400 on a $400 purchase.
-
Test Scores: If a student answered 12 out of 400 questions correctly on a test, their score would be 3%.
-
Proportional Reasoning: Understanding 3/100 allows for easy scaling. For example, if 3% of 400 is 12, then 3% of 800 would be 24, and 3% of 1200 would be 36. This demonstrates the power of proportional reasoning.
Further Exploration: Beyond Simplification
While simplifying 12/400 to 3/100 is often the most efficient approach, understanding the relationship between the original fraction and its simplified equivalent is crucial. The process of simplification doesn't change the inherent value; it simply provides a more concise and manageable representation. Consider the following:
-
Comparing Fractions: When comparing fractions, having them in their simplified form is often simpler. For example, comparing 12/400 to another fraction would be easier after simplification to 3/100.
-
Performing Calculations: Calculations involving 3/100 are typically easier and less prone to errors than calculations with 12/400. This is especially true when dealing with multiplication and division.
-
Understanding Proportions: The simplified form highlights the underlying proportional relationship. The ratio 3:100 is much easier to grasp than 12:400.
Frequently Asked Questions (FAQ)
Q1: Can 12/400 be simplified further than 3/100?
A1: No, 3/100 is the simplest form of the fraction 12/400 because the greatest common divisor of 3 and 100 is 1.
Q2: What is the reciprocal of 12/400?
A2: The reciprocal of a fraction is found by inverting the numerator and denominator. The reciprocal of 12/400 (or 3/100) is 400/12 (or 100/3).
Q3: How do I convert 12/400 to a percentage without simplifying first?
A3: You can convert directly: (12/400) x 100% = 3%. While simplifying first is often easier, it's not necessary.
Q4: Are there any other ways to simplify fractions besides finding the GCD?
A4: Yes, you can simplify fractions by repeatedly dividing both the numerator and denominator by common factors until no more common factors exist. This method is less efficient than using the GCD but achieves the same result.
Q5: Why is simplifying fractions important?
A5: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also provides a more concise and accurate representation of the value.
Conclusion: Mastering Fractions for Real-World Success
Understanding the fraction 12/400, and its various representations (3/100, 0.03, and 3%), is a valuable skill applicable in diverse fields. The process of simplification, conversion to decimals and percentages, and application to real-world problems emphasizes the importance of mastering fundamental mathematical concepts. By grasping these concepts, you equip yourself with tools to tackle various challenges efficiently and confidently. This knowledge extends far beyond simple arithmetic, laying a solid foundation for more advanced mathematical studies and practical problem-solving in numerous contexts. From interpreting survey data to understanding financial reports, the ability to work with fractions is an essential skill for navigating the complexities of everyday life.
Latest Posts
Latest Posts
-
Half Of 49
Sep 20, 2025
-
150lbs En Kg
Sep 20, 2025
-
Cecil J Sharp
Sep 20, 2025
-
30 Of 360
Sep 20, 2025
-
50g Of Butter
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 12 Of 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.