11 X Pi
interactiveleap
Sep 24, 2025 · 5 min read
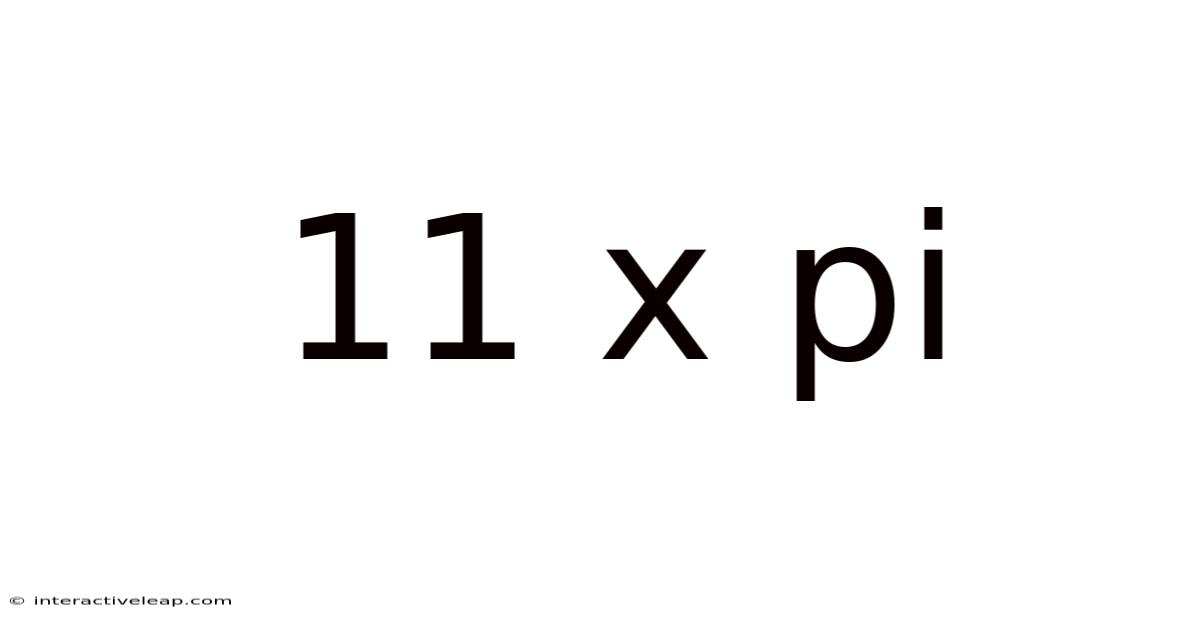
Table of Contents
Unraveling the Mystery of 11π: A Deep Dive into the Mathematical Constant
The number π (pi), approximately 3.14159, is arguably the most famous mathematical constant. It represents the ratio of a circle's circumference to its diameter and appears ubiquitously in various fields, from geometry and trigonometry to physics and engineering. But what about 11π? This seemingly simple multiplication hides a surprising depth of mathematical significance and practical applications. This article will explore the value of 11π, its calculation, its applications, and delve into some related mathematical concepts. We'll unravel the mystery behind this fascinating number, exploring its significance beyond a simple multiplication.
Understanding the Value of 11π
At its core, 11π is simply eleven times the value of pi. While π is an irrational number (meaning its decimal representation goes on forever without repeating), we can approximate its value to a desired level of accuracy. Using a common approximation of π ≈ 3.14159, we can calculate 11π as follows:
11 * 3.14159 ≈ 34.55749
However, this is just an approximation. The true value of 11π is an irrational number with an infinite number of non-repeating decimal places. The precision required for any specific application will dictate the number of decimal places needed for the calculation.
Calculating 11π: Methods and Precision
Several methods exist to calculate 11π to a high degree of accuracy. The most straightforward approach is to use a high-precision value of π from a mathematical software package or a high-precision calculator. These tools often employ sophisticated algorithms to compute π to thousands or even millions of decimal places.
Another approach involves using infinite series that converge to π. One famous example is the Leibniz formula for π:
π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
This series, while elegant, converges very slowly, meaning it requires many terms to achieve a high level of accuracy. More efficient algorithms, such as the Chudnovsky algorithm, are used in practice for calculating π to many decimal places. Once a highly accurate value of π is obtained, multiplying it by 11 provides an equally accurate approximation of 11π. The choice of method depends on the desired precision and computational resources available.
Applications of 11π in Real-World Scenarios
While 11π itself might not appear explicitly in many formulas, it frequently arises as an intermediate calculation in various applications where π is involved. Consider these examples:
-
Circumference Calculations: If we have a circle with a radius of 11/2 units, the circumference is given by 2πr = 2π(11/2) = 11π. This calculation is crucial in engineering, construction, and manufacturing, for instance, when determining the length of materials needed for circular structures or components.
-
Area Calculations: The area of an annulus (a ring-shaped region between two concentric circles) with outer radius R and inner radius r is given by π(R² - r²). If R = 6 and r = 5, the area is π(6² - 5²) = 11π. This calculation finds applications in various fields, including surveying and design.
-
Circular Sector Area: A sector is a part of a circle enclosed by two radii and an arc. The area of a sector with central angle θ (in radians) and radius r is given by (θ/2)r². If θ = 22 radians and r = 1, the area is (22/2)(1)² = 11π. This has implications in various calculations involving portions of circles.
-
Volume Calculations: Consider a cylinder with radius r = 11/2π and height h=2. The volume is given by πr²h = π(11/2π)²(2) = 121/2π = 11π(11/2π). While this seems contrived, it highlights that calculations involving π, especially multiplications like 11π, frequently appear in geometric volume calculations.
11π and Related Mathematical Concepts
The study of 11π connects to several key mathematical concepts:
-
Irrational Numbers: As mentioned earlier, both π and 11π are irrational numbers. This means they cannot be expressed as a ratio of two integers. The irrationality of π has been proven, and since multiplying an irrational number by a rational number (like 11) generally results in another irrational number, 11π is also irrational.
-
Approximations and Error Analysis: When working with irrational numbers, approximations are necessary. The accuracy of an approximation is crucial in many applications. Understanding error analysis is essential to ensure that the error introduced by using an approximation of 11π is within acceptable limits.
-
Series and Convergence: Infinite series provide powerful methods for computing π and, consequently, 11π to any desired accuracy. Studying the convergence rate of these series is essential for optimizing the computational efficiency of such calculations.
Frequently Asked Questions (FAQ)
-
Is 11π a transcendental number? Yes, since π is a transcendental number (a number that is not a root of any non-zero polynomial with rational coefficients), and multiplying a transcendental number by a non-zero rational number (like 11) results in another transcendental number, 11π is also transcendental.
-
How many decimal places of 11π are needed for practical applications? The required number of decimal places depends entirely on the application's precision requirements. For most engineering and scientific purposes, a few decimal places are sufficient. However, high-precision calculations in advanced mathematics or computer science may require many more.
-
Are there any special properties of 11π beyond its definition? No significant special properties of 11π are known beyond its direct relationship to π. Its mathematical significance lies primarily in its role as a result of a simple multiplication involving a fundamental mathematical constant.
-
Can 11π be expressed as a simple fraction? No, it cannot. As a multiple of an irrational number, it remains irrational and cannot be expressed as a ratio of two integers.
Conclusion: The Significance of Exploring 11π
While seemingly a simple mathematical expression, 11π serves as a valuable lens through which to explore fundamental concepts in mathematics. From understanding irrational numbers and approximation methods to appreciating the practical applications of π in various fields, the exploration of 11π reinforces the importance of mathematical precision and its vital role in scientific and technological advancements. Its seemingly straightforward nature belies its importance within broader mathematical frameworks, highlighting the depth and interconnectedness of mathematical ideas. By understanding 11π, we deepen our comprehension of the mathematical constant π and its profound influence across disciplines. The pursuit of understanding such seemingly simple mathematical concepts ultimately enriches our knowledge and expands our appreciation of the elegance and power of mathematics.
Latest Posts
Latest Posts
-
Symbols Of Courage
Sep 24, 2025
-
45kph To Mph
Sep 24, 2025
-
15 Of 42 00
Sep 24, 2025
-
90 Into Feet
Sep 24, 2025
-
Sellotape Dispenser Wheel
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 11 X Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.