100 X 3
interactiveleap
Sep 19, 2025 · 6 min read
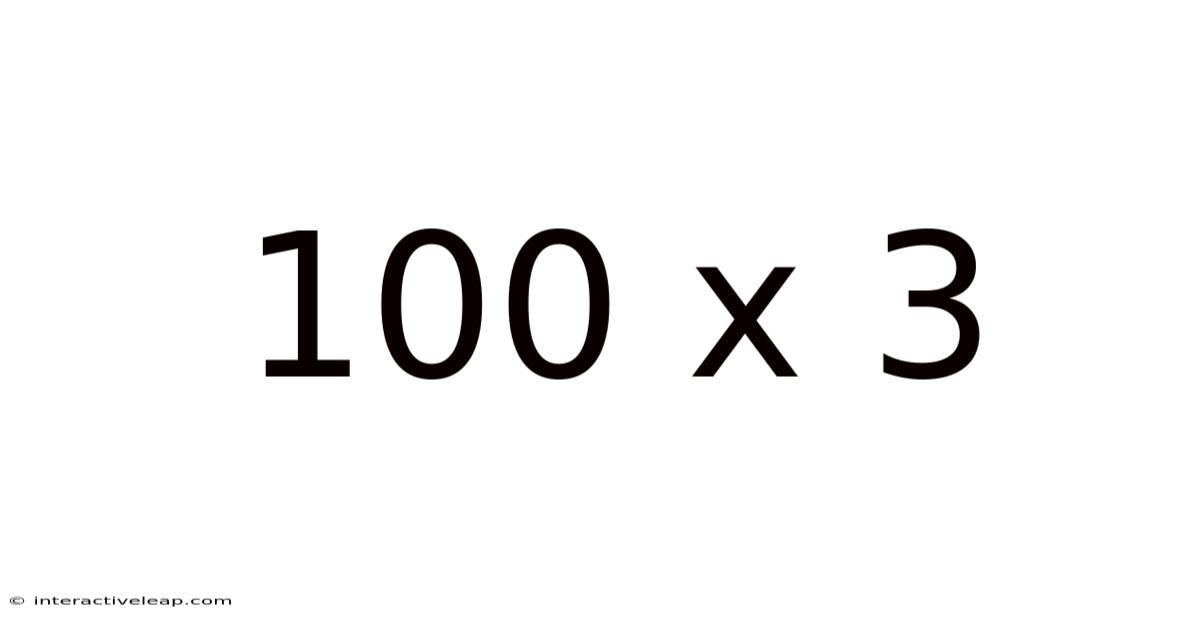
Table of Contents
Decoding 100 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple equation, 100 x 3, delving far beyond the basic answer to uncover the underlying mathematical principles, practical applications, and its significance in various fields. We'll journey from the fundamentals of multiplication to its role in advanced calculations, highlighting its relevance in everyday life and beyond. Understanding 100 x 3 isn't just about arriving at the answer; it's about grasping the power of multiplication as a fundamental building block of mathematics.
Understanding the Basics: What is Multiplication?
Multiplication, at its core, is repeated addition. When we say 100 x 3, we're essentially saying "add 100 to itself three times." This fundamental concept is crucial for understanding more complex mathematical operations. Visualizing this as three groups of 100 objects, like apples, cars, or even abstract units, can help solidify this understanding, especially for younger learners. This simple visual representation lays the foundation for grasping larger numbers and more complex multiplications.
100 x 3 = 100 + 100 + 100 = 300
This seemingly basic equation forms the base for many more complex mathematical problems. Mastering this fundamental concept is essential before moving on to more advanced topics.
Methods for Calculating 100 x 3
There are several approaches to calculate 100 x 3, catering to different skill levels and preferences:
-
Repeated Addition: As previously explained, adding 100 three times (100 + 100 + 100) yields the answer 300. This method is ideal for beginners to visualize the concept of multiplication.
-
Multiplication Table: Knowing the multiplication table is a vital skill. The table shows that 100 multiplied by 3 is 300. Regular practice with multiplication tables builds fluency and speed in calculations.
-
Mental Math: With practice, one can perform this calculation mentally. Recognizing that multiplying by 100 simply adds two zeros to the number being multiplied makes this calculation straightforward. 3 becomes 300. This develops mental agility and problem-solving skills.
-
Using a Calculator: For larger calculations or situations demanding speed and accuracy, a calculator is a helpful tool. However, relying solely on a calculator can hinder the development of fundamental mathematical skills.
Each of these methods contributes to a well-rounded understanding of multiplication and its application. The choice of method depends on the context and the individual's skillset.
100 x 3 in Different Number Systems
While the decimal system (base-10) is most commonly used, exploring 100 x 3 in other number systems provides valuable insights into the universality of mathematical principles.
-
Binary System (base-2): Converting 100 and 3 to binary, performing the multiplication, and then converting back to decimal offers a unique perspective. This exercise strengthens understanding of different number systems and their interrelation.
-
Hexadecimal System (base-16): Similar to the binary system, exploring 100 x 3 in the hexadecimal system showcases the adaptability of multiplication across different numerical bases.
While the actual calculation process differs, the fundamental concept of repeated addition remains consistent regardless of the number system employed.
Real-World Applications of 100 x 3
The seemingly simple equation, 100 x 3, finds its way into a surprising number of real-world scenarios:
-
Business and Finance: Calculating the total cost of three items priced at $100 each. This is a basic example, but the principle extends to calculating bulk discounts, inventory costs, or profits.
-
Engineering and Construction: Estimating material quantities. For example, if a project requires three units of a material costing $100 per unit, the total cost is easily calculated as 100 x 3.
-
Everyday Life: Determining the total price of three identical purchases, like three $100 concert tickets or three $100 online courses.
-
Scientific Calculations: Although 100 x 3 itself is a simple calculation, the underlying principle of multiplication is fundamental to complex scientific formulas and models used across various disciplines.
Expanding the Concept: Beyond 100 x 3
Understanding 100 x 3 allows us to explore broader concepts in mathematics:
-
Distributive Property: The equation can be used to illustrate the distributive property of multiplication over addition. For instance, 100 x (2 + 1) = (100 x 2) + (100 x 1) = 300.
-
Factors and Multiples: Understanding factors and multiples is crucial. 100 and 3 are factors of 300, while 300 is a multiple of both 100 and 3.
-
Prime Factorization: Breaking down numbers into their prime factors helps understand the building blocks of a number. While 300 isn't prime, its prime factorization provides valuable insights into its composition.
-
Algebra: The equation can be represented algebraically, such as 100x = 300, where x = 3. This transition to algebraic representation allows for solving more complex equations.
Addressing Common Misconceptions
Common mistakes in multiplication often arise from a lack of understanding of basic principles:
-
Incorrect Place Value: When dealing with larger numbers, errors can occur due to incorrect placement of digits. Careful attention to place value is crucial for accuracy.
-
Misunderstanding of Zero: Multiplying by 100 involves adding two zeros, a concept some students find challenging. Reinforcing the understanding of place value and the role of zero in multiplication helps address this.
-
Lack of Practice: Regular practice is essential to build fluency and accuracy in multiplication. Consistent practice using various methods strengthens understanding and reduces errors.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate 100 x 3?
A: The easiest way is likely mental math, recognizing that multiplying by 100 simply adds two zeros to the number being multiplied (3 becomes 300).
Q: Can I use a calculator to solve 100 x 3?
A: Yes, a calculator can provide a quick answer, but practicing mental calculation builds mathematical skills.
Q: What are the real-world applications of this simple multiplication problem?
A: This calculation finds application in various fields, from calculating simple costs to more complex calculations in finance, engineering, and scientific applications.
Q: What if I need to calculate 100 x 3.5?
A: This requires understanding decimal multiplication, which builds upon the foundation of whole number multiplication. You would multiply 100 by 3 and then 100 by 0.5 (half of 100) and add the results.
Conclusion: The Power of Simplicity
The seemingly simple equation 100 x 3 unlocks a vast landscape of mathematical concepts and real-world applications. It's not just about getting the answer (300); it's about understanding the process, appreciating the underlying principles, and recognizing its importance in various fields. Mastering basic arithmetic, like this multiplication, forms the foundation for tackling more advanced mathematical concepts and problem-solving in diverse areas of life. Consistent practice, exploring different methods, and applying the knowledge to real-world situations will solidify your understanding and build confidence in your mathematical abilities. The journey of understanding 100 x 3 is a microcosm of the broader mathematical journey, highlighting the importance of building a solid foundation through practice and exploration.
Latest Posts
Latest Posts
-
80 Of 24
Sep 19, 2025
-
Binary For 17
Sep 19, 2025
-
40cm To Mm
Sep 19, 2025
-
3 Of 80000
Sep 19, 2025
-
Plywood Sheet Cost
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 100 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.