10 Of 480
interactiveleap
Sep 13, 2025 · 5 min read
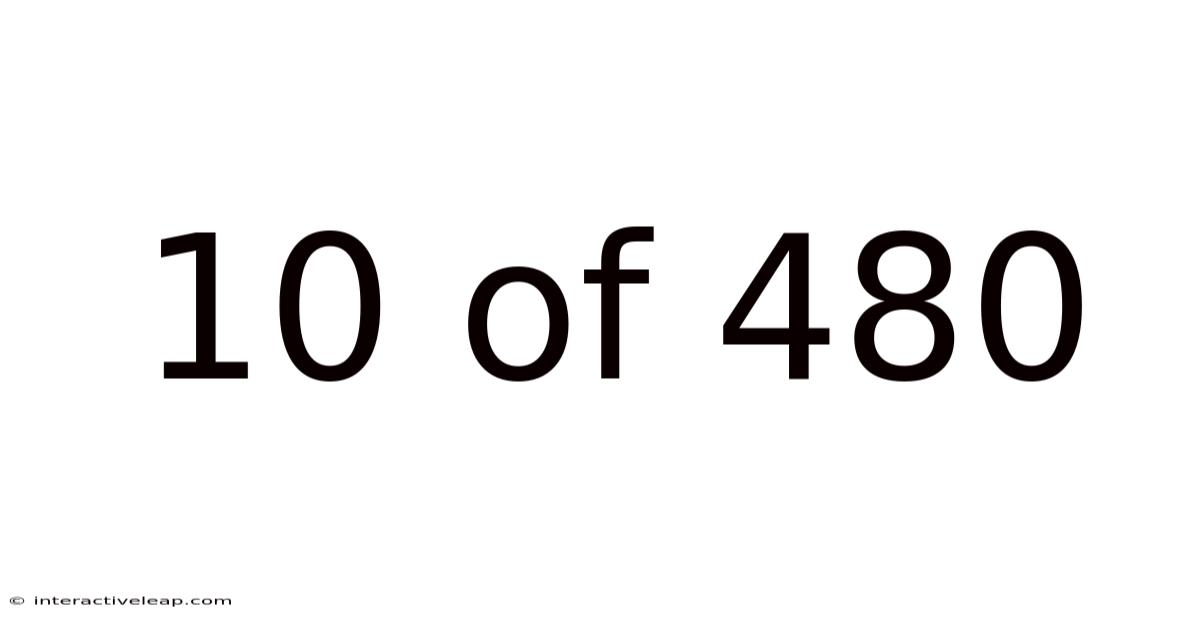
Table of Contents
Decoding the Enigma: Understanding the Fraction 10/480 and its Implications
The seemingly simple fraction 10/480 might appear insignificant at first glance. However, understanding this fraction and its various representations unlocks a deeper appreciation for fundamental mathematical concepts and their real-world applications. This article will explore the fraction 10/480 in detail, covering its simplification, decimal and percentage equivalents, applications in various fields, and addressing common questions and misconceptions. We'll also delve into the broader context of fraction manipulation and its importance in problem-solving.
Introduction: The Foundation of Fractions
Fractions represent parts of a whole. They are expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, 10/480 means 10 parts out of a total of 480 parts. Understanding fractions is crucial across numerous disciplines, from basic arithmetic to advanced calculus, engineering, and even cooking! Mastering fraction manipulation allows for accurate calculations and precise problem-solving.
Simplifying 10/480: Finding the Lowest Terms
Before delving deeper, let's simplify the fraction 10/480 to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator (10) and the denominator (480) and dividing both by it. The GCD of 10 and 480 is 10.
Therefore:
10/480 = (10 ÷ 10) / (480 ÷ 10) = 1/48
Simplifying a fraction doesn't change its value; it merely represents it in a more concise and manageable form. This simplified form, 1/48, is much easier to work with in calculations.
Decimal and Percentage Equivalents: Different Perspectives
To gain a more intuitive understanding, let's convert 1/48 into its decimal and percentage equivalents.
-
Decimal Equivalent: Dividing the numerator (1) by the denominator (48) yields approximately 0.020833.
-
Percentage Equivalent: Multiplying the decimal equivalent by 100 gives us approximately 2.0833%.
These conversions provide alternative ways to represent the same value, making it easier to interpret in different contexts. For instance, a percentage is often more readily understandable in everyday scenarios. Understanding the interchangeability of fractions, decimals, and percentages is a key skill in mathematics.
Applications in Real-World Scenarios: From Percentages to Proportions
The fraction 10/480, and its simplified form 1/48, finds practical applications in various situations:
-
Percentage Calculations: Imagine you scored 10 points out of a possible 480 points on a test. The fraction 10/480, simplified to 1/48, represents your performance. Converting this to a percentage (approximately 2.08%) gives a clearer picture of your score.
-
Proportions and Ratios: If a recipe calls for 480 grams of flour and you only want to make a smaller portion using 10 grams of flour, the ratio 10/480 (or 1/48) indicates the proportion you need to scale down all other ingredients.
-
Probability: If you have a bag containing 480 marbles, and 10 of them are red, the probability of randomly picking a red marble is 10/480, or 1/48.
-
Engineering and Design: Engineers frequently use ratios and proportions in design calculations. A simplified fraction like 1/48 could represent a scale factor in a blueprint or a ratio of components in a machine.
These examples highlight the versatility of fractions and their importance in practical problem-solving across diverse fields.
Expanding the Understanding: Fraction Operations
Let's briefly touch upon common operations involving fractions:
-
Addition and Subtraction: To add or subtract fractions, they must have a common denominator. For example, adding 1/48 and 2/48 is straightforward: (1+2)/48 = 3/48, which can then be further simplified.
-
Multiplication: Multiplying fractions is simple: multiply the numerators together and the denominators together. For example, (1/48) * (2/3) = 2/144, which can be simplified.
-
Division: Dividing fractions involves inverting the second fraction and multiplying. For instance, (1/48) ÷ (2/3) = (1/48) * (3/2) = 3/96, which can be simplified.
These basic operations are foundational for more complex mathematical calculations.
Frequently Asked Questions (FAQ): Addressing Common Concerns
Here are some common questions regarding fractions and their manipulation:
-
Q: Why is simplifying fractions important?
- A: Simplifying makes fractions easier to understand and use in calculations. It reduces the risk of errors and presents the information in a more concise form.
-
Q: How do I find the greatest common divisor (GCD)?
- A: Several methods exist, including listing factors or using the Euclidean algorithm. For smaller numbers, listing factors is often sufficient.
-
Q: What if the fraction has a large denominator?
- A: Even with large denominators, the principles of simplification and conversion remain the same. It might require more effort to find the GCD, but the process is consistent.
-
Q: Are there online tools to help with fraction calculations?
- A: Yes, many online calculators and tools can assist with fraction simplification, conversion, and operations. However, understanding the underlying principles is crucial for problem-solving.
Conclusion: The Power of a Simple Fraction
The seemingly simple fraction 10/480, reduced to its simplest form of 1/48, unveils a deeper understanding of fundamental mathematical concepts. From its decimal and percentage equivalents to its numerous applications across various fields, this fraction exemplifies the practical significance of fractional arithmetic. Mastering fraction manipulation is not merely about solving equations; it’s about developing critical thinking skills applicable in countless real-world scenarios. By understanding the concepts outlined here, you’ve taken a significant step towards mastering this fundamental aspect of mathematics and enhancing your problem-solving abilities. Remember, the power of mathematics lies in its ability to simplify complex situations and provide clear, concise solutions, and fractions are a vital tool in this process. The journey of understanding fractions is a continuous one, with each new challenge offering an opportunity to deepen your knowledge and appreciation of this fundamental concept. Continue to explore and expand your understanding, and you will undoubtedly reap the rewards in your mathematical pursuits.
Latest Posts
Latest Posts
-
Poacher Turned Gamekeeper
Sep 13, 2025
-
7 5 To Fraction
Sep 13, 2025
-
Admission Point Score
Sep 13, 2025
-
2 Of 400
Sep 13, 2025
-
155lb To Kg
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 480 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.