10 Of 450
interactiveleap
Sep 14, 2025 · 5 min read
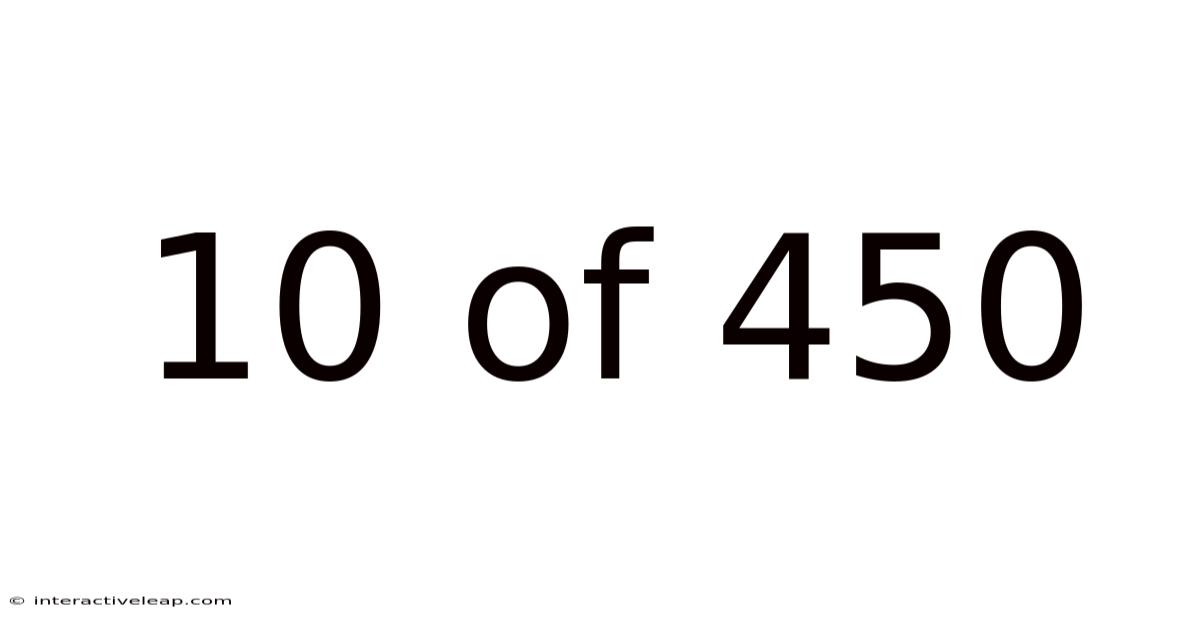
Table of Contents
Decoding the Enigma: Understanding the Fraction 10/450 and its Implications
The seemingly simple fraction 10/450 might appear insignificant at first glance. However, a deeper dive reveals its potential to illustrate fundamental mathematical concepts and their applications in various fields. This article will explore the meaning of 10/450, its simplification, conversion to decimal and percentage forms, real-world applications, and delve into related mathematical ideas, ensuring a comprehensive understanding for readers of all backgrounds.
Introduction: What does 10/450 Represent?
10/450, pronounced as "ten over four hundred and fifty," represents a ratio or a part of a whole. It signifies that out of a total of 450 units, we are considering only 10 of them. Understanding this basic representation is crucial to grasp the fraction's significance and further manipulations. This seemingly small fraction can be used to represent various proportions in diverse contexts, from calculating percentages in finance to understanding probability in statistics. The ability to simplify, convert, and interpret fractions like 10/450 is a fundamental skill across many disciplines.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before delving into further calculations, it's crucial to simplify 10/450 to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (10) and the denominator (450). The GCD is the largest number that divides both numbers without leaving a remainder.
In this case, the GCD of 10 and 450 is 10. We can determine this through prime factorization:
- 10 = 2 x 5
- 450 = 2 x 3² x 5²
The common factors are 2 and 5, resulting in a GCD of 2 x 5 = 10.
Dividing both the numerator and the denominator by the GCD (10), we simplify the fraction:
10 ÷ 10 / 450 ÷ 10 = 1/45
Therefore, 10/450 is equivalent to the much simpler fraction 1/45. This simplified form is easier to work with for further calculations and comparisons.
Converting to Decimal Form: Understanding Decimal Equivalents
To convert the fraction 1/45 to its decimal equivalent, we perform long division: 1 divided by 45. This yields a recurring decimal:
1 ÷ 45 ≈ 0.02222...
The decimal representation is approximately 0.0222. The ellipsis (...) indicates that the digit '2' repeats infinitely. In practical applications, we often round the decimal to a specific number of decimal places, depending on the required level of accuracy. For example, rounding to three decimal places gives us 0.022.
Converting to Percentage Form: Expressing Proportion as a Percentage
The percentage form expresses the fraction as a proportion of 100. To convert 1/45 to a percentage, we multiply the decimal equivalent by 100:
0.0222... x 100 ≈ 2.22%
Therefore, 10/450 represents approximately 2.22%. This percentage form provides a readily understandable representation of the proportion.
Real-World Applications: Where do we see 10/450?
While 10/450 might not be a commonly encountered fraction in everyday life in its raw form, the underlying concepts and its simplified equivalent (1/45) appear frequently:
-
Probability: Imagine a bag containing 45 marbles, with only 1 marble being red. The probability of picking the red marble at random is 1/45, directly reflecting the simplified fraction.
-
Surveys and Statistics: If a survey of 450 people reveals that only 10 favor a particular product, the proportion of those favoring the product is 10/450, or 2.22%. This data helps understand market trends and consumer preferences.
-
Resource Allocation: Consider a project requiring 450 units of a certain resource. If only 10 units are currently available, the proportion of available resources is 10/450, or 1/45. This helps assess project feasibility and potential delays.
-
Financial Calculations: In situations involving calculating interest, discounts, or returns on investments, the principles of working with fractions and percentages are fundamental. A small percentage change in a large number can result in significant outcomes.
-
Mixing and Concentrations: In chemistry or cooking, proportions play a vital role. If a recipe calls for 450ml of liquid and you only use 10ml of a certain ingredient, the concentration of that ingredient is 10/450 or 1/45.
Mathematical Extensions: Exploring Related Concepts
Understanding 10/450 opens doors to exploring several interconnected mathematical concepts:
-
Ratio and Proportion: The fraction fundamentally represents a ratio (10:450) and can be used in proportion problems to find unknown quantities. For example, if the ratio of men to women in a group is 1:45, and there are 10 men, how many women are there? The answer can be found using cross-multiplication.
-
Percentage Change: Understanding the percentage equivalent of the fraction enables calculations of percentage increase or decrease. If the number of units increases from 10 to 20, this signifies a 100% increase.
-
Fractional Arithmetic: Working with fractions necessitates mastering addition, subtraction, multiplication, and division of fractions. These operations are essential for solving problems involving ratios and proportions.
Frequently Asked Questions (FAQ)
-
Q: Can 10/450 be simplified further than 1/45?
- A: No, 1/45 is the simplest form of the fraction because 1 and 45 share no common divisors other than 1.
-
Q: How do I convert a percentage back to a fraction?
- A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 2.22% becomes 2.22/100, which simplifies to 111/5000.
-
Q: What if the numerator and denominator had no common factors?
- A: If the GCD is 1, the fraction is already in its simplest form. There's no further simplification needed.
-
Q: Are there any online tools to help simplify fractions?
- A: Yes, many online calculators and websites are available to simplify fractions, convert fractions to decimals and percentages, and perform other fraction-related calculations. However, understanding the underlying process is crucial for building mathematical proficiency.
Conclusion: The Significance of a Seemingly Simple Fraction
While 10/450 initially appears to be a straightforward fraction, a thorough examination reveals its rich mathematical implications. Its simplification to 1/45 highlights the importance of finding the greatest common divisor. The conversion to decimal and percentage forms illustrates the versatility of representing proportions. Moreover, the various real-world applications underscore the relevance of fraction understanding across diverse fields. By mastering the manipulation and interpretation of such fractions, we enhance our problem-solving skills and mathematical reasoning abilities, paving the way for deeper exploration of more complex mathematical concepts. The seemingly simple 10/450 serves as a potent reminder of the fundamental power and practical utility of basic mathematical principles.
Latest Posts
Latest Posts
-
67inches In Feet
Sep 14, 2025
-
Cleaning Of Floors
Sep 14, 2025
-
55miles In Km
Sep 14, 2025
-
Poison Tree Emoji
Sep 14, 2025
-
80z In Ml
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.