10 2 Simplified
interactiveleap
Sep 14, 2025 · 7 min read
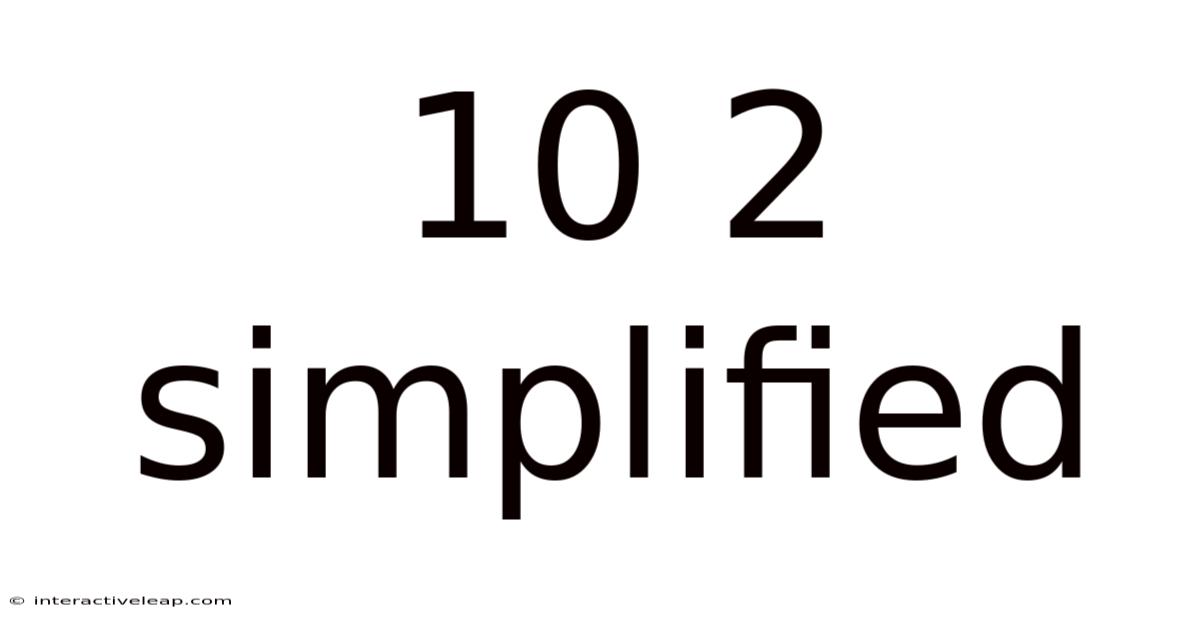
Table of Contents
Decoding 10<sup>2</sup>: A Comprehensive Guide to Exponents and Their Applications
Understanding exponents, often represented by a superscript number (like the '2' in 10<sup>2</sup>), is fundamental to mathematics and science. This seemingly simple concept, however, unlocks doors to a world of complex calculations and powerful problem-solving techniques. This article will provide a comprehensive explanation of 10<sup>2</sup>, its calculation, real-world applications, and delve deeper into the broader concept of exponents and their properties. We’ll explore everything from basic arithmetic to more advanced mathematical concepts, making this a valuable resource for students and anyone looking to strengthen their understanding of exponential notation.
What Does 10<sup>2</sup> Mean?
At its core, 10<sup>2</sup> represents 10 multiplied by itself two times. This is often read as "ten squared" or "ten to the power of two." The base number (10) is the number being multiplied, and the exponent (2) indicates how many times the base is multiplied by itself. Therefore, the calculation is straightforward: 10 x 10 = 100.
So, 10<sup>2</sup> = 100. This might seem basic, but grasping this fundamental principle is crucial for understanding more complex exponential expressions.
Understanding Exponents: A Deeper Dive
Exponents, also known as powers or indices, are a concise way of representing repeated multiplication. The general form is b<sup>n</sup>, where 'b' is the base and 'n' is the exponent. This means 'b' is multiplied by itself 'n' times.
For instance:
- 2<sup>3</sup> = 2 x 2 x 2 = 8 (two cubed or two to the power of three)
- 5<sup>4</sup> = 5 x 5 x 5 x 5 = 625 (five to the power of four)
- 1<sup>5</sup> = 1 x 1 x 1 x 1 x 1 = 1 (one to any power is always one)
Special Cases and Properties of Exponents
Several rules govern the manipulation of exponents, making complex calculations simpler. Understanding these properties is essential for mastering exponential notation.
-
Product of Powers: When multiplying two terms with the same base, add the exponents: b<sup>m</sup> * b<sup>n</sup> = b<sup>(m+n)</sup>. For example, 2<sup>3</sup> * 2<sup>2</sup> = 2<sup>(3+2)</sup> = 2<sup>5</sup> = 32.
-
Quotient of Powers: When dividing two terms with the same base, subtract the exponents: b<sup>m</sup> / b<sup>n</sup> = b<sup>(m-n)</sup>. For example, 2<sup>5</sup> / 2<sup>2</sup> = 2<sup>(5-2)</sup> = 2<sup>3</sup> = 8.
-
Power of a Power: When raising a power to another power, multiply the exponents: (b<sup>m</sup>)<sup>n</sup> = b<sup>(mn)</sup>. For example, (2<sup>3</sup>)<sup>2</sup> = 2<sup>(32)</sup> = 2<sup>6</sup> = 64.
-
Power of a Product: When raising a product to a power, raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>. For example, (2*3)<sup>2</sup> = 2<sup>2</sup> * 3<sup>2</sup> = 4 * 9 = 36.
-
Power of a Quotient: When raising a quotient to a power, raise both the numerator and denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>. For example, (2/3)<sup>2</sup> = 2<sup>2</sup>/3<sup>2</sup> = 4/9.
-
Zero Exponent: Any non-zero base raised to the power of zero equals 1: b<sup>0</sup> = 1. For example, 10<sup>0</sup> = 1.
-
Negative Exponent: A negative exponent indicates the reciprocal of the base raised to the positive exponent: b<sup>-n</sup> = 1/b<sup>n</sup>. For example, 10<sup>-2</sup> = 1/10<sup>2</sup> = 1/100 = 0.01.
Applications of 10<sup>2</sup> and Exponents in Real Life
The concept of exponents, particularly with base 10, appears frequently in various aspects of daily life and scientific fields. Understanding 10<sup>2</sup> and related concepts is essential for navigating many situations.
-
Area Calculations: The area of a square with side length 10 units is 10<sup>2</sup> = 100 square units. This extends to calculating areas of larger squares or other geometric shapes involving squares.
-
Metric System: The metric system relies heavily on powers of 10. For example, a square meter (1m<sup>2</sup>) is 100 square centimeters (100cm<sup>2</sup>), reflecting the relationship 10<sup>2</sup>. Similarly, understanding powers of 10 is crucial for converting between kilometers, meters, centimeters, and millimeters.
-
Scientific Notation: Scientific notation uses powers of 10 to represent very large or very small numbers concisely. For example, the speed of light (approximately 300,000,000 meters per second) can be expressed as 3 x 10<sup>8</sup> m/s. This makes handling such numbers significantly easier.
-
Compound Interest: Compound interest calculations involve exponents. The formula A = P(1 + r/n)<sup>nt</sup> uses exponents to determine the final amount (A) based on the principal amount (P), interest rate (r), number of times interest is compounded per year (n), and the number of years (t).
-
Computer Science: Binary numbers (base 2) are fundamental to computer science. Understanding exponents in base 2 is essential for representing data and performing calculations within a computer system. For example, the number 10 in binary is 1010<sub>2</sub> which equals 12<sup>3</sup> + 02<sup>2</sup> + 12<sup>1</sup> + 02<sup>0</sup> = 8 + 0 + 2 + 0 = 10.
Solving Problems Involving 10<sup>2</sup> and Exponents
Let's look at a few example problems to solidify our understanding of exponents:
Problem 1: Calculate the area of a square with sides of length 10 meters.
Solution: The area of a square is side * side, or side<sup>2</sup>. Therefore, the area is 10<sup>2</sup> = 100 square meters.
Problem 2: Simplify the expression: (10<sup>3</sup> * 10<sup>2</sup>) / 10<sup>4</sup>.
Solution: Using the rules of exponents, we add exponents for multiplication and subtract exponents for division: 10<sup>(3+2-4)</sup> = 10<sup>1</sup> = 10.
Problem 3: Convert 5,000,000 into scientific notation.
Solution: 5,000,000 can be written as 5 x 10<sup>6</sup>.
Frequently Asked Questions (FAQ)
Q: What is the difference between 10<sup>2</sup> and 2<sup>10</sup>?
A: 10<sup>2</sup> means 10 multiplied by itself twice (10 x 10 = 100). 2<sup>10</sup> means 2 multiplied by itself ten times (2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 1024). They are distinctly different values.
Q: How do I calculate numbers with very large exponents?
A: For very large exponents, calculators or computer software are typically used. Many scientific calculators and mathematical software packages can handle extremely large exponential calculations.
Q: Are there negative exponents for bases other than 10?
A: Yes, negative exponents apply to any non-zero base. For example, 2<sup>-3</sup> = 1/2<sup>3</sup> = 1/8 = 0.125.
Q: Why is 10 a commonly used base for exponents?
A: Base 10 is commonly used because of its direct relationship to our decimal number system. It simplifies calculations and representations, particularly in scientific notation and metric system conversions.
Conclusion: Mastering the Power of Exponents
Understanding exponents, even seemingly simple ones like 10<sup>2</sup>, opens up a world of possibilities in mathematics and science. From calculating areas and volumes to understanding scientific notation and compound interest, the applications are far-reaching. By mastering the fundamental principles and rules governing exponents, you'll build a strong foundation for tackling more complex mathematical challenges and deepening your understanding of the world around you. The ability to confidently work with exponents is a vital skill for success in many academic and professional fields. Remember to practice regularly, utilizing the rules and properties discussed above to solidify your understanding and build your problem-solving skills.
Latest Posts
Latest Posts
-
Poison Tree Emoji
Sep 14, 2025
-
80z In Ml
Sep 14, 2025
-
Allison Breakfast Club
Sep 14, 2025
-
80 Of 4
Sep 14, 2025
-
25 Of 50
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 10 2 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.