10.00 X 20
interactiveleap
Sep 14, 2025 · 5 min read
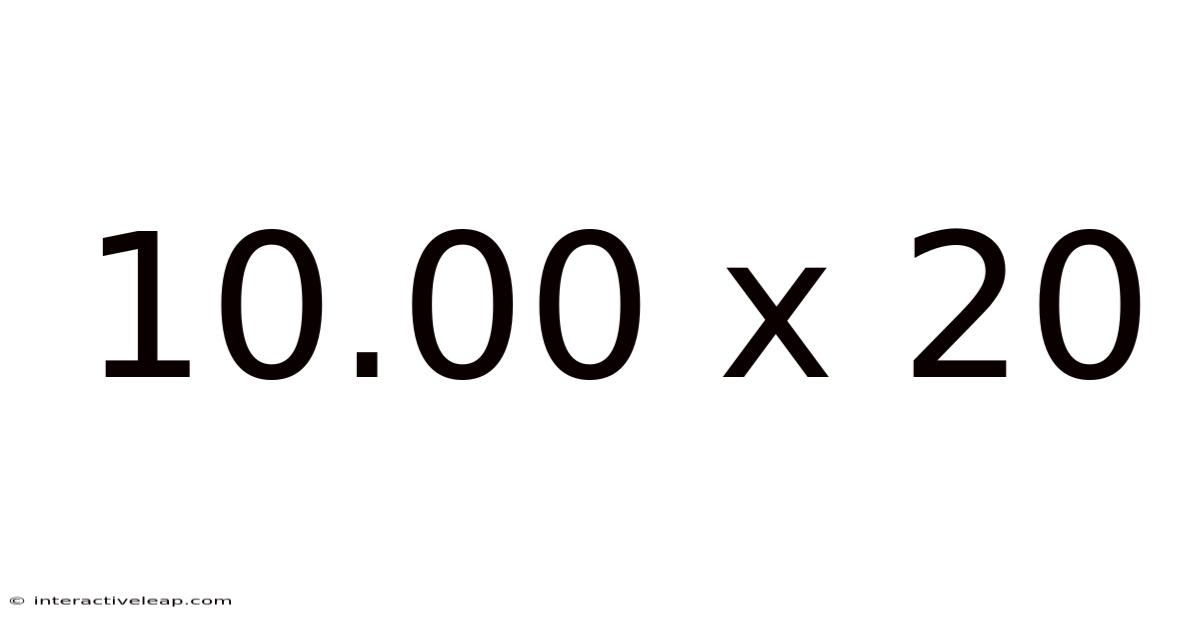
Table of Contents
Decoding 10.00 x 20: Exploring Multiplication, Decimal Operations, and Real-World Applications
This article delves into the seemingly simple calculation of 10.00 x 20, unraveling its mathematical underpinnings and showcasing its relevance in various real-world scenarios. We will explore the fundamentals of multiplication, specifically focusing on operations involving decimals, and demonstrate how this particular calculation applies to everyday life, from simple budgeting to complex financial modeling. Understanding this seemingly basic calculation provides a strong foundation for more advanced mathematical concepts.
Understanding the Fundamentals of Multiplication
Multiplication is a fundamental arithmetic operation representing repeated addition. When we say 10.00 x 20, we're essentially asking: "What is the sum of twenty 10.00s?" This can be visualized as adding 10.00 twenty times: 10.00 + 10.00 + 10.00… and so on. However, multiplication provides a much more efficient way to arrive at the answer.
Working with Decimals in Multiplication
The number 10.00 includes a decimal point. This decimal point signifies a fractional part of a whole number. In this case, 10.00 is equivalent to 10. Including the extra zeros after the decimal point often clarifies the context, especially in financial applications where precision is paramount. When multiplying numbers with decimals, the standard rules of multiplication still apply. We first perform the multiplication as if the decimal point wasn't there:
1000 x 20 = 20000
Next, we count the total number of digits after the decimal point in the original numbers being multiplied. In our case, 10.00 has two digits after the decimal point (00). We then place the decimal point in the result, such that there are two digits after the decimal point. In this instance, there are already two zeros at the end, so we place the decimal point to move those digits to the right side:
20000 becomes 200.00, which simplifies to 200.
Therefore, 10.00 x 20 = 200.
Step-by-Step Calculation of 10.00 x 20
Let's break down the calculation methodically:
- Ignore the decimal: Initially, disregard the decimal point in 10.00, treating it as 1000.
- Perform standard multiplication: Multiply 1000 by 20: 1000 x 20 = 20000
- Account for the decimal: Since 10.00 has two digits after the decimal, we add two zeros to the result to the right of the decimal place.
- Place the decimal point: The result 20000 becomes 200.00 (or simply 200).
Alternative Calculation Methods
While the above method is straightforward, other approaches can be used to solve 10.00 x 20:
- Distributive Property: We can break down 20 into 2 x 10. This allows us to calculate 10.00 x 2 = 20.00, and then multiply the result by 10: 20.00 x 10 = 200.00
- Using Fractions: We can represent 10.00 as 10/1 and 20 as 20/1. Then, we multiply the numerators (10 x 20 = 200) and the denominators (1 x 1 = 1). This simplifies to 200.
- Mental Math: With practice, one can perform this multiplication mentally, recognizing that multiplying by 20 is equivalent to multiplying by 2 and then by 10.
Real-World Applications of 10.00 x 20
The calculation 10.00 x 20 has practical applications across various domains:
- Finance: Imagine purchasing 20 items priced at $10.00 each. The total cost would be 10.00 x 20 = $200.00. This calculation is essential for budgeting, cost analysis, and inventory management.
- Measurements: If you have 20 boxes, each measuring 10.00 centimeters in height, the combined height would be 200 centimeters. This is crucial in fields like construction, engineering, and packaging.
- Scientific Calculations: In scientific experiments, multiplying quantities is frequent. For example, if a reaction produces 20 units of a substance, and each unit weighs 10.00 grams, the total weight would be 200 grams.
- Business and Economics: This calculation is fundamental in numerous business scenarios, such as calculating revenue from sales, determining the cost of materials, and analyzing production output. For instance, if a company sells 20 units of a product priced at $10 each, the revenue will be $200.
Expanding the Concept: Multiplication with Different Decimals
Understanding 10.00 x 20 helps us grasp multiplication with various decimal numbers. Let's consider a few examples:
- 5.50 x 20: This involves multiplying 550 by 20 to get 11000. Since there are two digits after the decimal in 5.50, we get 110.00, or simply 110.
- 12.75 x 20: Multiply 1275 by 20, yielding 25500. Since 12.75 has two decimal places, the result is 255.00, or 255.
- 0.50 x 20: Multiply 50 by 20 to get 1000. With two decimal places, the result becomes 10.00, or 10.
Frequently Asked Questions (FAQ)
Q: Why is it important to understand the placement of the decimal point in multiplication?
A: Correct decimal placement ensures accuracy in the final answer. Incorrect placement can lead to significant errors, especially in financial and scientific calculations.
Q: Can I use a calculator to solve 10.00 x 20?
A: Absolutely! Calculators are useful tools for performing multiplication quickly and accurately, especially with larger or more complex numbers. However, understanding the underlying principles remains crucial.
Q: What if I have to multiply numbers with more decimal places?
A: The process remains the same. Multiply the numbers without considering the decimal points, then count the total number of digits after the decimal points in the original numbers. Place the decimal point accordingly in the final result.
Q: Are there any shortcuts for multiplying numbers by 20?
A: Yes, multiplying by 20 is equivalent to multiplying by 2 and then by 10. This often simplifies the calculation.
Conclusion
The seemingly simple calculation of 10.00 x 20 provides a gateway to understanding fundamental mathematical principles, particularly multiplication involving decimals. This concept extends far beyond basic arithmetic, finding practical applications in various aspects of our daily lives, from personal finance to complex scientific research. Mastering this calculation, along with its underlying principles, empowers us to tackle more advanced mathematical challenges with confidence and precision. Remember to always pay close attention to decimal placement to ensure accuracy in your results. By understanding the "why" behind the calculation, you build a more robust and intuitive understanding of mathematics, preparing you for more intricate problems in the future.
Latest Posts
Latest Posts
-
20 Of 21
Sep 14, 2025
-
Calcium Carbonate Hydrochloric
Sep 14, 2025
-
Factorise 6x 4
Sep 14, 2025
-
181cm In Inches
Sep 14, 2025
-
Light And Warmth
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 10.00 X 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.