1.5 X 10
interactiveleap
Sep 20, 2025 · 7 min read
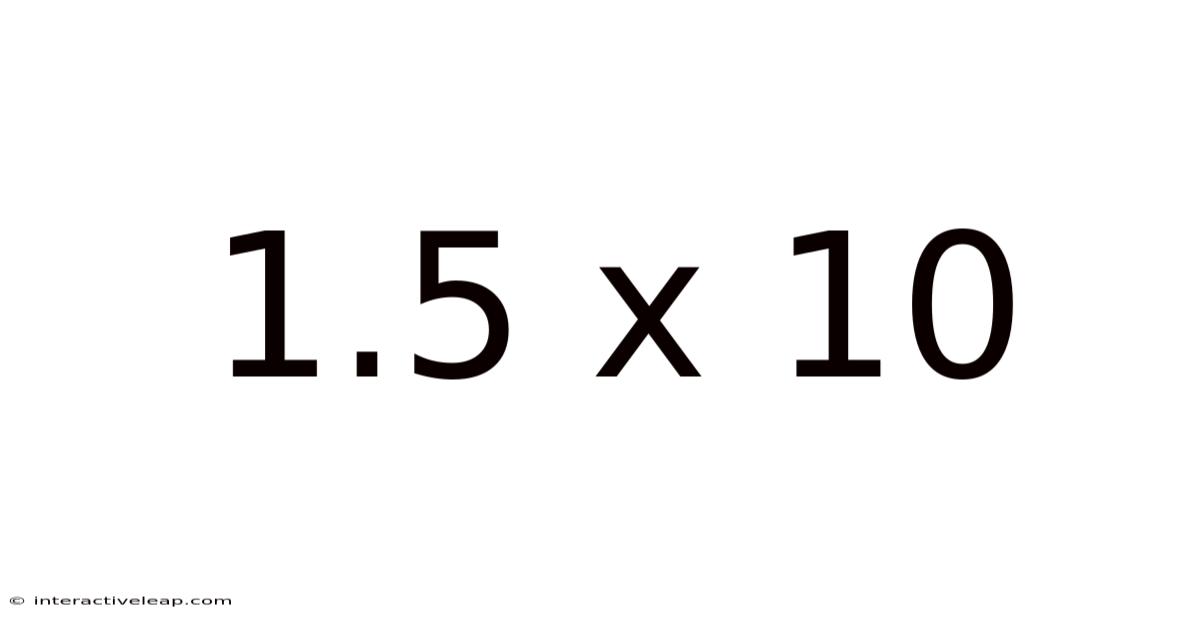
Table of Contents
Decoding 1.5 x 10: Exploring Scientific Notation and its Applications
Scientific notation, a cornerstone of scientific and mathematical fields, provides a concise way to represent extremely large or extremely small numbers. Understanding this notation is crucial for various disciplines, from physics and chemistry to engineering and computer science. This article will delve deep into the meaning of 1.5 x 10, explain the underlying principles of scientific notation, and explore its widespread applications. We'll also tackle common misconceptions and address frequently asked questions. Learning about scientific notation empowers you to comprehend and manipulate vast numerical scales with ease.
Understanding Scientific Notation: A Foundation
Scientific notation expresses numbers in the form a x 10<sup>b</sup>, where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer (a whole number, positive, negative, or zero). This representation simplifies the handling of numbers with many digits, making calculations and comparisons significantly easier. The exponent 'b' indicates how many places the decimal point needs to be moved to obtain the standard form of the number.
Let's break down the components of 1.5 x 10:
-
1.5 (or 'a'): This is the coefficient, or the mantissa. It’s always a number between 1 and 10.
-
10 (the base): This is the base of the exponential notation. It's always 10 in scientific notation.
-
0 (or 'b'): This is the exponent, indicating the power of 10. In this case, 10<sup>0</sup> equals 1, so 1.5 x 10<sup>0</sup> simplifies to 1.5.
Therefore, 1.5 x 10<sup>0</sup> is simply another way of writing the number 1.5. While seemingly straightforward in this specific example, the power of scientific notation becomes much more apparent when dealing with numbers far larger or smaller than 1.5.
Expanding the Concept: Beyond 1.5 x 10<sup>0</sup>
To fully grasp the utility of scientific notation, let's explore examples with different exponents:
-
1.5 x 10<sup>1</sup>: This means 1.5 multiplied by 10 to the power of 1, which is 15. The exponent of 1 tells us to move the decimal point one place to the right.
-
1.5 x 10<sup>2</sup>: This equals 150. The decimal point moves two places to the right.
-
1.5 x 10<sup>3</sup>: This equals 1500. The decimal point moves three places to the right.
Now let's consider negative exponents:
-
1.5 x 10<sup>-1</sup>: This means 1.5 multiplied by 10 to the power of -1, which is equivalent to 1.5 divided by 10, resulting in 0.15. The negative exponent indicates that the decimal point moves one place to the left.
-
1.5 x 10<sup>-2</sup>: This equals 0.015. The decimal point moves two places to the left.
-
1.5 x 10<sup>-3</sup>: This equals 0.0015. The decimal point moves three places to the left.
Practical Applications: Where Scientific Notation Shines
Scientific notation's true value lies in its ability to handle extremely large and small numbers encountered in various scientific fields:
-
Astronomy: Distances in space are often expressed in scientific notation. For example, the distance to the Sun is approximately 1.5 x 10<sup>8</sup> kilometers. This notation avoids writing out a long string of zeros. Similarly, the mass of stars and planets, measured in kilograms, frequently requires scientific notation for convenient representation.
-
Chemistry: In chemistry, the number of atoms or molecules in a given amount of substance (Avogadro's number) is approximately 6.022 x 10<sup>23</sup>. This enormous number is easily manageable using scientific notation. Similarly, the concentrations of solutions, often expressed in molarity (moles per liter), frequently utilize scientific notation for expressing very dilute or very concentrated solutions.
-
Physics: In physics, quantities such as Planck's constant (6.626 x 10<sup>-34</sup> joule-seconds), which describes the smallest possible unit of energy, are naturally expressed using scientific notation. Calculations involving subatomic particles and their interactions constantly involve extremely small numbers.
-
Computer Science: Representing very large or very small numbers in computer memory often employs scientific notation or its variations. Floating-point numbers, a key data type in computer programming, leverage similar principles to efficiently handle a wide range of numerical values.
-
Engineering: The size of integrated circuits or the power of large-scale systems often require scientific notation for easy understanding and calculation. For example, the frequency of a signal might be expressed in Hertz (Hz) using scientific notation, as might the capacity of a data storage device (gigabytes, terabytes, etc.).
Converting to and from Scientific Notation
Converting a number to scientific notation involves the following steps:
-
Move the decimal point until the number is between 1 and 10.
-
Count the number of places you moved the decimal point. This number becomes the exponent.
-
If you moved the decimal point to the left, the exponent is positive.
-
If you moved the decimal point to the right, the exponent is negative.
-
Write the number in the form a x 10<sup>b</sup>.
Converting from scientific notation to standard form simply involves moving the decimal point according to the exponent:
-
A positive exponent means moving the decimal point to the right.
-
A negative exponent means moving the decimal point to the left.
Calculations with Scientific Notation
Performing calculations with scientific notation involves applying the rules of exponents and multiplication.
-
Multiplication: Multiply the coefficients and add the exponents. For instance, (2.5 x 10<sup>3</sup>) x (3 x 10<sup>2</sup>) = (2.5 x 3) x 10<sup>(3+2)</sup> = 7.5 x 10<sup>5</sup>.
-
Division: Divide the coefficients and subtract the exponents. For instance, (6 x 10<sup>5</sup>) / (2 x 10<sup>2</sup>) = (6/2) x 10<sup>(5-2)</sup> = 3 x 10<sup>3</sup>.
-
Addition and Subtraction: Before adding or subtracting numbers in scientific notation, ensure they have the same exponent. Adjust the coefficients and exponents accordingly before performing the operation. For example, to add 2.5 x 10<sup>3</sup> and 3 x 10<sup>2</sup>, we rewrite 3 x 10<sup>2</sup> as 0.3 x 10<sup>3</sup>, then add: 2.5 x 10<sup>3</sup> + 0.3 x 10<sup>3</sup> = 2.8 x 10<sup>3</sup>.
Common Misconceptions and Pitfalls
-
Incorrect Coefficient: Remember that the coefficient ('a') must always be between 1 and 10 (exclusive).
-
Exponent Errors: Carefully track the sign and magnitude of the exponent during calculations.
-
Significant Figures: When performing calculations, pay attention to the rules of significant figures to maintain accuracy.
-
Mixing Scientific Notation and Standard Form: Avoid mixing the two notations mid-calculation; convert to a single form before performing operations.
Frequently Asked Questions (FAQ)
Q: What if the coefficient is not between 1 and 10?
A: Adjust the coefficient and exponent accordingly to meet the scientific notation standard. For example, 25 x 10<sup>3</sup> should be rewritten as 2.5 x 10<sup>4</sup>.
Q: How do I handle very large numbers with many zeros?
A: Count the number of places you need to move the decimal point to the left to obtain a coefficient between 1 and 10. This count becomes the positive exponent.
Q: How do I handle very small numbers with many zeros after the decimal point?
A: Count the number of places you need to move the decimal point to the right to obtain a coefficient between 1 and 10. This count becomes the negative exponent.
Q: Can I use scientific notation with numbers that are not very large or very small?
A: Yes, you can. For example, 2.5 x 10<sup>0</sup> is a perfectly valid representation of 2.5. However, it is generally not necessary to use scientific notation for numbers easily expressed in standard form.
Q: Why is scientific notation important?
A: It significantly simplifies the representation, manipulation, and comparison of extremely large or small numbers, common in many scientific and engineering disciplines, saving space and reducing errors.
Conclusion: Mastering the Power of Scientific Notation
Scientific notation offers a powerful and efficient tool for handling numbers across vast scales. Mastering this system is essential for comprehending and working with data in various scientific and technical fields. By understanding its principles, applying the rules correctly, and avoiding common pitfalls, you can effectively utilize scientific notation to simplify complex calculations and foster a deeper understanding of numerical magnitude in countless applications. While the example of 1.5 x 10<sup>0</sup> might seem basic initially, it lays the foundation for understanding this invaluable tool that unlocks the secrets of the universe's vast numerical landscape.
Latest Posts
Latest Posts
-
First Words Dictionary
Sep 20, 2025
-
Spherical Crossword Clue
Sep 20, 2025
-
500ml In L
Sep 20, 2025
-
Kpa Tp Psi
Sep 20, 2025
-
X 6 8
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1.5 X 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.