1/4 Of 36
interactiveleap
Sep 17, 2025 · 5 min read
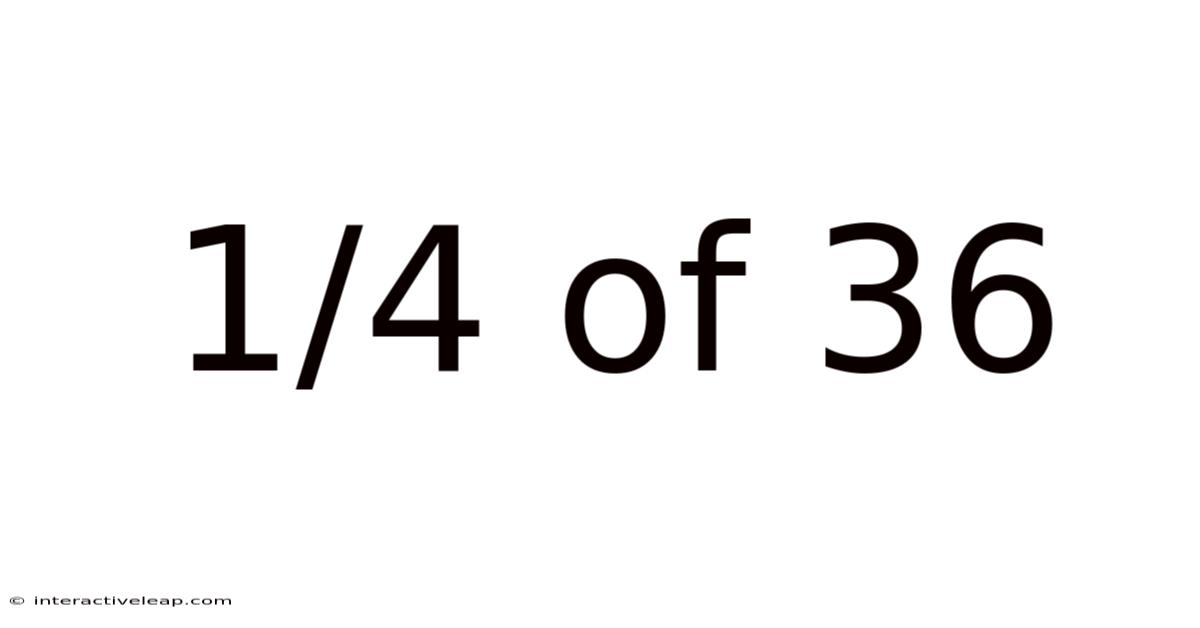
Table of Contents
Unlocking the Power of Fractions: A Deep Dive into 1/4 of 36
Finding a quarter of a number, like calculating 1/4 of 36, might seem like a simple arithmetic problem. But understanding this seemingly basic operation opens a door to a much wider world of mathematical concepts, from fractions and percentages to ratios and proportions. This article will explore the solution to 1/4 of 36, delve into the underlying mathematical principles, and examine real-world applications, making this fundamental concept accessible and engaging for everyone, regardless of their mathematical background.
Understanding Fractions: The Building Blocks of Calculation
Before tackling the problem of finding 1/4 of 36, let's briefly review the fundamentals of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. In the fraction 1/4, the numerator is 1, and the denominator is 4. This means we're considering one part out of four equal parts.
Calculating 1/4 of 36: A Step-by-Step Approach
There are several ways to calculate 1/4 of 36. Let's explore the most common methods:
Method 1: Direct Multiplication
The most straightforward method involves directly multiplying the fraction by the whole number. We can express 36 as a fraction by placing it over 1 (36/1). Then, we multiply the numerators together and the denominators together:
(1/4) * (36/1) = (1 * 36) / (4 * 1) = 36/4
Now, we simplify the fraction by dividing the numerator by the denominator:
36/4 = 9
Therefore, 1/4 of 36 is 9.
Method 2: Division
Alternatively, we can interpret "1/4 of 36" as dividing 36 into four equal parts. This is because finding a fraction of a number is essentially dividing that number by the denominator of the fraction.
36 / 4 = 9
This method directly yields the answer: 9.
Method 3: Using Decimal Equivalents
We can convert the fraction 1/4 into its decimal equivalent. Since 1/4 represents one quarter, its decimal equivalent is 0.25. Then, we multiply 36 by 0.25:
36 * 0.25 = 9
This method provides the same result, reinforcing the accuracy of our calculations.
Expanding the Concept: Beyond 1/4 of 36
Understanding how to calculate 1/4 of 36 is a stepping stone to understanding more complex fractional calculations. Let's explore some related concepts:
-
Finding other fractions of 36: Using the same methods, we can easily calculate other fractions of 36, such as 1/2 of 36 (which is 18), 3/4 of 36 (which is 27), or any other fraction. The core principle remains the same: multiplication or division depending on your preferred method.
-
Calculating percentages: Percentages are essentially fractions with a denominator of 100. For instance, 25% is equivalent to 25/100, which simplifies to 1/4. Therefore, calculating 25% of 36 is the same as calculating 1/4 of 36, resulting in 9.
-
Proportions and ratios: Fractions are fundamental to understanding proportions and ratios. A proportion shows the relationship between two ratios. For example, the ratio of 1 to 4 (1:4) is proportional to the ratio of 9 to 36 (9:36), both representing the fraction 1/4. This concept is widely used in various fields, including scaling recipes, map-making, and engineering.
Real-World Applications: Where Fractions Matter
The ability to calculate fractions, especially simple ones like 1/4, is essential in various real-world scenarios:
-
Cooking and baking: Recipes often involve fractions, requiring you to calculate the correct amounts of ingredients. For example, if a recipe calls for 1/4 cup of sugar, you'll need to know how to measure that accurately.
-
Money management: Understanding fractions helps in managing finances. For example, calculating sales tax, discounts, or splitting bills equally often involves fractional calculations.
-
Measurement and construction: In construction and other trades, precise measurements are critical. Often, measurements involve fractions of inches or centimeters.
-
Data analysis: Fractions are fundamental in statistics and data analysis, representing proportions and probabilities.
Addressing Common Misconceptions
A common misconception involves confusion between adding and multiplying fractions. Adding fractions requires a common denominator, while multiplying fractions involves multiplying the numerators and denominators directly. Understanding this difference is crucial for accurate calculations.
Another common error is incorrectly simplifying fractions. It's important to find the greatest common divisor (GCD) of the numerator and denominator to simplify the fraction to its lowest terms. For example, 12/16 simplifies to 3/4 by dividing both the numerator and denominator by 4 (their GCD).
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate 1/4 of a number?
A: The easiest way is often dividing the number by 4. This directly gives you one-quarter of the original value.
Q: Can I use a calculator to calculate 1/4 of 36?
A: Yes, you can. Simply enter 0.25 * 36 or 36 / 4 into your calculator.
Q: What if I need to calculate a more complex fraction of 36, such as 7/8?
A: You can use the same principles: multiply 36 by the numerator (7) and then divide by the denominator (8). (7/8) * 36 = (7 * 36) / 8 = 252 / 8 = 31.5
Q: How are fractions related to percentages?
A: Percentages are just fractions with a denominator of 100. For example, 25% is the same as 25/100, which simplifies to 1/4.
Conclusion: Mastering the Fundamentals
Calculating 1/4 of 36, while seemingly straightforward, provides a solid foundation for understanding a range of mathematical concepts. By mastering this basic operation, you build confidence and proficiency in working with fractions, percentages, proportions, and ratios—skills valuable in various academic and real-world contexts. Remember, the key is to understand the underlying principles rather than just memorizing procedures. With practice and a clear understanding of the concepts, you'll confidently navigate the world of fractions and unlock their powerful applications. So, next time you encounter a fractional calculation, remember the simple elegance and wide-ranging utility of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
38 4celsius To Fahrenheit
Sep 17, 2025
-
Electronic Variable Orifice
Sep 17, 2025
-
47 Pounds Kg
Sep 17, 2025
-
68 95kg In Stone
Sep 17, 2025
-
2 5 2
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.