1/4 Of 20
interactiveleap
Sep 16, 2025 · 5 min read
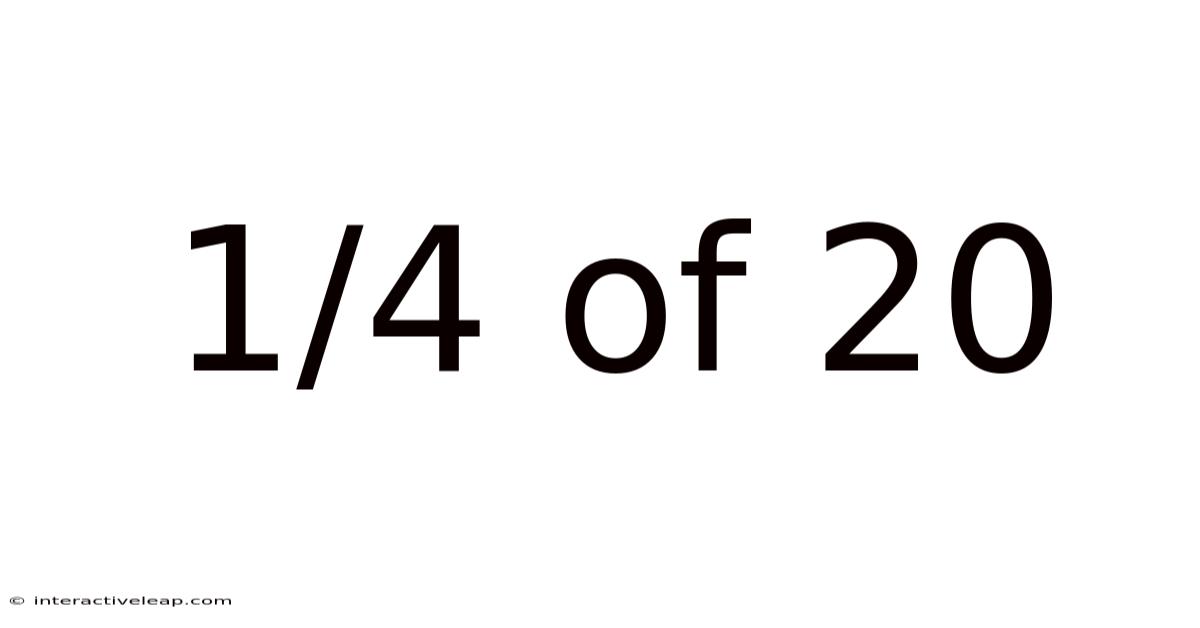
Table of Contents
Decoding 1/4 of 20: A Deep Dive into Fractions, Percentages, and Real-World Applications
Understanding fractions and percentages is a fundamental skill in mathematics, with wide-ranging applications in everyday life. This article delves into the seemingly simple calculation of "1/4 of 20," exploring its various interpretations, the underlying mathematical principles, and its relevance across different contexts. We'll cover the basic calculation, explore different methods of solving the problem, discuss the connection to percentages, and finally, examine real-world examples to solidify your understanding. This comprehensive guide aims to leave you not just with the answer but with a deeper grasp of fractional arithmetic and its practical implications.
Understanding Fractions: A Quick Refresher
Before we tackle "1/4 of 20," let's review the basics of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In our example, 1/4, the numerator is 1 and the denominator is 4. This means we have 1 part out of a total of 4 equal parts.
Calculating 1/4 of 20: The Simple Approach
The simplest way to calculate 1/4 of 20 is to perform the following calculation:
(1/4) * 20 = 20/4 = 5
We multiply the fraction (1/4) by the whole number (20). This is equivalent to dividing 20 into 4 equal parts. The result, 5, represents one of those four equal parts. Therefore, 1/4 of 20 is 5.
Alternative Methods: Exploring Different Approaches
While the direct multiplication method is the most efficient, let's explore other approaches to demonstrate the versatility of fractional calculations:
-
Division: Since finding a fraction of a number is essentially division, we can directly divide 20 by 4: 20 ÷ 4 = 5. This reinforces the concept that finding 1/4 of a number is the same as dividing the number by 4.
-
Decimal Conversion: We can convert the fraction 1/4 into its decimal equivalent (0.25). Then, we can multiply 0.25 by 20: 0.25 * 20 = 5. This demonstrates the interchangeability between fractions and decimals.
-
Visual Representation: Imagine a pizza cut into four equal slices. If the whole pizza represents 20, each slice represents 20/4 = 5. Therefore, one slice (1/4) represents 5. This visual approach helps solidify the concept for those who learn better through visual aids.
The Connection to Percentages: Understanding Proportions
Fractions and percentages are intrinsically linked. A percentage is simply a fraction expressed as parts per hundred. To convert 1/4 into a percentage, we divide the numerator by the denominator and multiply by 100:
(1/4) * 100 = 25%
This means that 1/4 is equivalent to 25%. Therefore, calculating 25% of 20 also yields the same result:
(25/100) * 20 = 5
This highlights the interconnectedness of fractions and percentages, offering alternative ways to approach the problem.
Real-World Applications: Seeing the Practicality
The concept of "1/4 of 20" isn't confined to abstract mathematical problems. It has numerous practical applications in various fields:
-
Cooking & Baking: A recipe calls for 20 ounces of flour, and the instructions require only 1/4 of the amount for a specific step. Understanding this fraction allows you to accurately measure 5 ounces of flour.
-
Finance: If you have a $20 bill and want to save 1/4 of it, you'll save $5. This simple calculation helps in budgeting and financial planning.
-
Shopping: A store offers a 25% discount on a $20 item. Knowing that 25% is equivalent to 1/4, you can quickly calculate the discount as $5.
-
Time Management: If you have 20 minutes for a task and want to dedicate only 1/4 of that time to a sub-task, you'll allocate 5 minutes. This helps in effective time allocation.
-
Geometry and Measurement: If you're working with a 20-meter long rope and need a piece that's 1/4 of its length, you'll cut a 5-meter piece.
-
Data Analysis: If a survey shows that 1/4 of 20 respondents prefer a particular product, this translates to 5 respondents, providing valuable insights for market research.
Beyond the Basics: Exploring More Complex Fractions
While we focused on 1/4 of 20, let's extend our understanding to other fractions and more complex scenarios. Consider the following examples:
-
Finding 3/4 of 20: This involves multiplying (3/4) * 20 = 15. It means we take three out of four equal parts of 20.
-
Finding 1/5 of 20: This is calculated as (1/5) * 20 = 4. This involves dividing 20 into five equal parts.
-
Finding a fraction of a fraction: This involves multiplying fractions, for example, finding (1/2) of (1/4) of 20. This would be calculated as (1/2) * (1/4) * 20 = 2.5.
These examples highlight the versatility of fractional calculations and their applicability to diverse problems.
Frequently Asked Questions (FAQ)
-
What is the easiest way to calculate a fraction of a number? The easiest way is typically direct multiplication. Multiply the fraction by the number.
-
How do I convert a fraction to a percentage? Divide the numerator by the denominator and multiply the result by 100.
-
Can I use decimals instead of fractions? Yes, you can convert fractions to decimals and use them in calculations.
-
What if the fraction results in a decimal? Decimal results are perfectly acceptable and often more practical in certain contexts.
-
Are there any online tools to help with fraction calculations? Yes, many online calculators and educational websites can assist with fraction calculations.
Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions is a crucial skill, not just for academic success, but also for navigating everyday life. This article explored the seemingly simple calculation of "1/4 of 20," demonstrating its different approaches, its connection to percentages, and its diverse applications across multiple fields. By mastering the concepts discussed here, you'll not only be able to solve such problems efficiently but also develop a deeper understanding of mathematical principles and their practical relevance. Remember, the key to mastering fractions lies in consistent practice and applying the concepts to real-world scenarios. So, go ahead, try out different problems, and watch your understanding grow!
Latest Posts
Latest Posts
-
Map In Classroom
Sep 16, 2025
-
2000lbs To Kg
Sep 16, 2025
-
30 Of 21
Sep 16, 2025
-
50 Of 13
Sep 16, 2025
-
86 3kg In Stone
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.