1/4 Divided 3
interactiveleap
Sep 17, 2025 · 5 min read
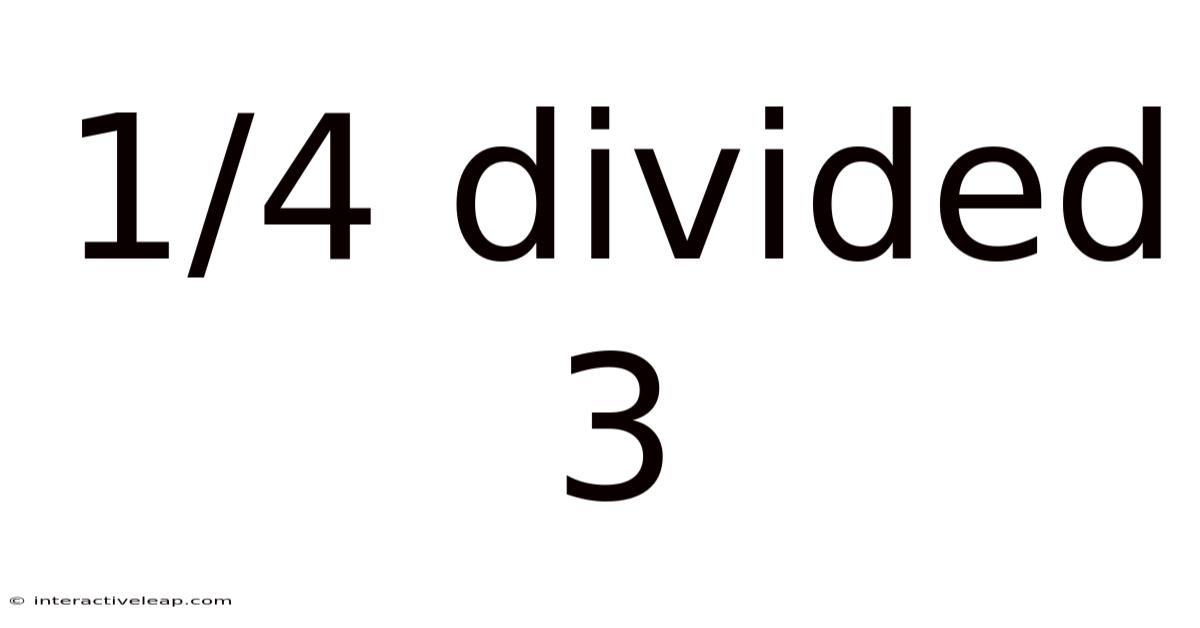
Table of Contents
Decoding 1/4 Divided by 3: A Comprehensive Guide to Fraction Division
Understanding fraction division can seem daunting at first, but with a clear approach, it becomes a straightforward process. This article will delve into the seemingly simple calculation of 1/4 divided by 3, providing a comprehensive explanation suitable for learners of all levels. We'll explore various methods, explain the underlying mathematical principles, and address common misconceptions. By the end, you'll not only know the answer but also understand the why behind the solution, empowering you to tackle similar fraction division problems with confidence.
Introduction: Unpacking the Problem
The problem, 1/4 divided by 3 (written as 1/4 ÷ 3), asks us to determine how many times the fraction 1/4 fits into the whole number 3. This seemingly simple problem highlights the fundamental principles of fraction division. Many students find fractions challenging, but with a systematic approach and a solid understanding of the concepts, mastering fraction division becomes achievable. We will examine multiple approaches to solving this problem, ensuring a comprehensive understanding of the underlying mechanics. This guide will also cover frequently asked questions and address common pitfalls encountered while working with fractions.
Method 1: The "Keep, Change, Flip" Method (Reciprocal)
This is arguably the most popular method for dividing fractions. It's a shortcut based on the mathematical principles of reciprocals and multiplication. Here's how it works:
- Keep: Keep the first fraction as it is: 1/4.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip (find the reciprocal of) the second fraction. Since 3 can be written as 3/1, its reciprocal is 1/3.
Therefore, the problem becomes: 1/4 × 1/3
Now, multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 × 1) / (4 × 3) = 1/12
Therefore, 1/4 divided by 3 equals 1/12.
Method 2: Visual Representation
Visualizing the problem can be incredibly helpful, particularly for those who prefer a more intuitive approach. Imagine a pizza cut into four equal slices. 1/4 represents one of these slices. The problem asks us to divide this single slice into three equal parts. Each of these smaller parts represents 1/12 of the original pizza.
Therefore, dividing 1/4 by 3 results in 1/12. This visual method reinforces the answer obtained using the "Keep, Change, Flip" method.
Method 3: Converting to Decimal (For Added Understanding)
While the fraction method is generally preferred for accuracy and clarity, converting the fraction to a decimal can provide a different perspective.
First, convert 1/4 to a decimal: 1/4 = 0.25
Then, divide the decimal by 3: 0.25 ÷ 3 ≈ 0.08333...
Converting this decimal back to a fraction:
0.08333... is approximately 1/12.
This method, although less precise without rounding, helps solidify the understanding that dividing a fraction by a whole number results in a smaller fraction.
Mathematical Explanation: The Rationale Behind the "Keep, Change, Flip" Method
The "Keep, Change, Flip" method is not just a trick; it's rooted in solid mathematical principles. Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a number is simply 1 divided by that number. For example:
- The reciprocal of 3 is 1/3.
- The reciprocal of 2/5 is 5/2.
Therefore, when we divide 1/4 by 3, we are essentially multiplying 1/4 by the reciprocal of 3, which is 1/3. This leads us back to the same solution: (1/4) × (1/3) = 1/12.
Expanding the Concept: Dividing Fractions by Other Fractions
The "Keep, Change, Flip" method is equally applicable when dividing a fraction by another fraction. For example, let's consider 2/5 divided by 1/2:
- Keep: 2/5
- Change: ÷ becomes ×
- Flip: 1/2 becomes 2/1
The problem now becomes: (2/5) × (2/1) = 4/5
Therefore, 2/5 divided by 1/2 equals 4/5. This demonstrates the versatility and power of this method for handling various fraction division problems.
Addressing Common Misconceptions
-
Confusing Division with Subtraction: A common mistake is to subtract the divisor from the dividend instead of dividing. Remember, division is about finding how many times one number fits into another.
-
Incorrectly Flipping the Wrong Fraction: Always flip the second fraction (the divisor), not the first fraction (the dividend).
-
Forgetting to Simplify: After multiplying, always simplify the resulting fraction to its lowest terms. For instance, if the result is 4/8, simplify it to 1/2.
Frequently Asked Questions (FAQs)
- Q: Why does the "Keep, Change, Flip" method work?
A: It works because dividing by a number is equivalent to multiplying by its reciprocal. This fundamental principle underpins the entire method.
- Q: Can I use a calculator to solve fraction division problems?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for solving problems without a calculator and for developing a strong mathematical foundation.
- Q: What if the divisor is a mixed number (e.g., 1 1/2)?
A: Convert the mixed number into an improper fraction first. For example, 1 1/2 becomes 3/2. Then, apply the "Keep, Change, Flip" method.
- Q: What if I get a complex fraction as a result?
A: Simplify the complex fraction by multiplying the numerator by the reciprocal of the denominator. For example, (1/2)/(3/4) can be simplified to (1/2) x (4/3) = 2/3
Conclusion: Mastering Fraction Division
Dividing fractions, even seemingly simple ones like 1/4 divided by 3, requires a clear understanding of the underlying principles. This article has explored multiple methods – the "Keep, Change, Flip" method, visual representation, and decimal conversion – to provide a comprehensive understanding of the process. By grasping these methods and addressing common misconceptions, you'll build a solid foundation for tackling more complex fraction division problems with confidence and accuracy. Remember that practice is key; the more you work with fractions, the more comfortable and proficient you will become. The initial challenge of understanding fractions will eventually transform into a mastery that strengthens your mathematical skills and problem-solving abilities.
Latest Posts
Latest Posts
-
70 Of 32
Sep 17, 2025
-
Decimal Of 5 9
Sep 17, 2025
-
Liter Water Weight
Sep 17, 2025
-
Best Nail Wraps
Sep 17, 2025
-
77 1kg In Stone
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Divided 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.