0.4 X 5
interactiveleap
Sep 25, 2025 · 6 min read
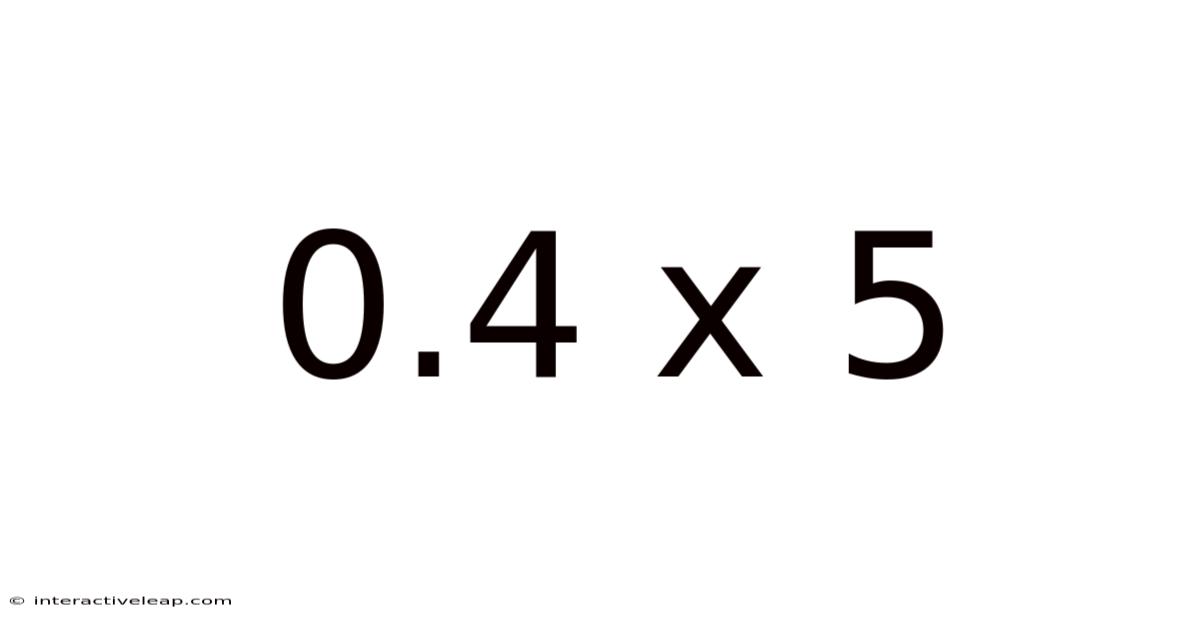
Table of Contents
Unpacking 0.4 x 5: A Deep Dive into Decimal Multiplication
This article explores the seemingly simple calculation of 0.4 x 5, delving beyond the immediate answer to understand the underlying mathematical principles and practical applications. We'll uncover the various methods for solving this problem, examine the concept of decimals and fractions, and explore how this type of calculation is used in everyday life and advanced mathematical concepts. Understanding 0.4 x 5 isn't just about getting the right answer; it's about grasping the fundamental building blocks of arithmetic and developing a deeper appreciation for numbers.
Introduction: The Significance of Simple Calculations
At first glance, 0.4 x 5 appears trivial. However, mastering this seemingly basic calculation is crucial for building a solid foundation in mathematics. It touches upon key concepts like decimal multiplication, the relationship between decimals and fractions, and the importance of understanding place value. This seemingly simple equation provides a springboard for exploring more complex mathematical ideas and real-world problem-solving. We will dissect this calculation methodically, explaining each step and providing context for a complete understanding.
Method 1: Direct Decimal Multiplication
The most straightforward method involves directly multiplying the decimal by the whole number. Remember, when multiplying decimals, you initially ignore the decimal point.
- Ignore the decimal: Treat 0.4 as 4.
- Multiply: Perform the multiplication: 4 x 5 = 20.
- Replace the decimal: Now, consider the number of digits after the decimal point in the original decimal number (0.4). There's one digit after the decimal. Therefore, place the decimal point one place from the right in the result (20). This gives us 2.0, or simply 2.
Therefore, 0.4 x 5 = 2.
Method 2: Converting to Fractions
Decimals and fractions are intrinsically linked. Converting 0.4 to a fraction provides an alternative approach to solving this problem.
- Convert to a fraction: 0.4 can be written as 4/10 (four-tenths). This is because the digit 4 is in the tenths place. You can simplify this fraction by dividing both the numerator and denominator by their greatest common divisor, which is 2. This simplifies to 2/5.
- Multiply the fractions: Now, multiply the fraction by 5: (2/5) x 5 = (2 x 5) / 5 = 10/5.
- Simplify the fraction: Finally, simplify the resulting fraction: 10/5 = 2.
This method demonstrates the equivalence between decimals and fractions and offers another path to the same solution.
Method 3: Repeated Addition
Multiplication can be understood as repeated addition. This approach offers a visual and conceptual understanding of the calculation.
0.4 x 5 can be interpreted as adding 0.4 five times: 0.4 + 0.4 + 0.4 + 0.4 + 0.4 = 2.0
This method is particularly helpful for visualizing the multiplication process and reinforcing the fundamental link between addition and multiplication.
Understanding Decimal Place Value
The concept of place value is fundamental to understanding decimal numbers and calculations involving them. In the number 0.4, the digit 4 represents four-tenths (4/10). Understanding this place value is crucial when multiplying decimals. The position of the decimal point dictates the magnitude of each digit.
Expanding on Decimals and Fractions: A Deeper Dive
The seamless conversion between decimals and fractions highlights their interconnectedness. Decimals are simply a convenient way to represent fractions with denominators that are powers of 10 (10, 100, 1000, etc.). This interchangeability is powerful and allows us to leverage the strengths of each representation when solving problems. For instance, some calculations are easier to visualize or perform using fractions, while others are more straightforward with decimals.
-
Converting Decimals to Fractions: To convert a decimal to a fraction, write the decimal as a fraction with a denominator that is a power of 10. The number of digits after the decimal point determines the power of 10. For example, 0.45 becomes 45/100, and 0.123 becomes 123/1000.
-
Converting Fractions to Decimals: To convert a fraction to a decimal, divide the numerator by the denominator. For example, 1/4 = 0.25, and 3/8 = 0.375.
Real-World Applications of 0.4 x 5 and Similar Calculations
While seemingly simple, the calculation of 0.4 x 5, and its underlying principles, finds applications in various real-world scenarios:
- Shopping: Calculating the cost of 5 items priced at $0.40 each.
- Measurement: Determining the total length of 5 pieces of wood, each measuring 0.4 meters long.
- Baking: Calculating the amount of an ingredient needed if a recipe calls for 0.4 cups and you need to make 5 times the recipe.
- Finance: Calculating a 40% discount (0.4) on a $5 item.
- Science: Many scientific calculations involve decimals and require a solid understanding of multiplication with decimals.
Frequently Asked Questions (FAQs)
-
What if the decimal had more digits? The principle remains the same. Multiply as you would with whole numbers, then count the total number of digits after the decimal points in the original numbers. This determines the number of places to move the decimal point in the final answer from the right. For example, 0.45 x 5 would be: 45 x 5 = 225. Then, since there are two digits after the decimal point in 0.45, the answer is 2.25.
-
Why is it important to understand decimal multiplication? Decimal multiplication forms the basis of many more complex calculations in algebra, calculus, and other advanced mathematical fields. It also has numerous practical applications in everyday life, from financial calculations to scientific measurements.
-
What are some common mistakes to avoid when multiplying decimals? The most common mistake is misplacing the decimal point in the final answer. Always count the total number of decimal places in the numbers you're multiplying.
-
Can I use a calculator? Calculators are useful tools, especially for more complex calculations. However, understanding the underlying mathematical principles is crucial for problem-solving and developing mathematical intuition. A calculator provides the answer, but understanding the method ensures you can solve the problem independently.
Beyond the Basics: Exploring Advanced Concepts
The seemingly simple equation 0.4 x 5 opens doors to more complex mathematical concepts. It serves as a building block for understanding:
- Algebra: Applying this knowledge to algebraic equations involving variables and decimals.
- Calculus: Understanding limits and derivatives, which frequently involve calculations with decimals.
- Statistics: Analyzing data involving decimals and percentages.
Conclusion: Mastering the Fundamentals
The calculation 0.4 x 5, though seemingly straightforward, offers a wealth of learning opportunities. By exploring the different methods of solving this problem – direct multiplication, fraction conversion, and repeated addition – we gain a deeper understanding of decimals, fractions, place value, and the fundamental principles of multiplication. This understanding extends far beyond the immediate answer, forming a crucial foundation for more complex mathematical concepts and real-world applications. Mastering this seemingly simple equation is a significant step towards building a robust mathematical foundation and confidence in tackling more challenging problems in the future. Remember, even the most complex mathematical concepts are built upon a foundation of simpler principles. A strong grasp of the fundamentals, such as understanding 0.4 x 5, empowers you to tackle more advanced mathematical concepts with ease and confidence.
Latest Posts
Latest Posts
-
Flamingo Bird Food
Sep 25, 2025
-
Bunnies With Guns
Sep 25, 2025
-
Yellow Red Colour
Sep 25, 2025
-
6 5inch In Cm
Sep 25, 2025
-
Alsatian Vs Rottweiler
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 0.4 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.