0.35 To Percentage
interactiveleap
Sep 19, 2025 · 5 min read
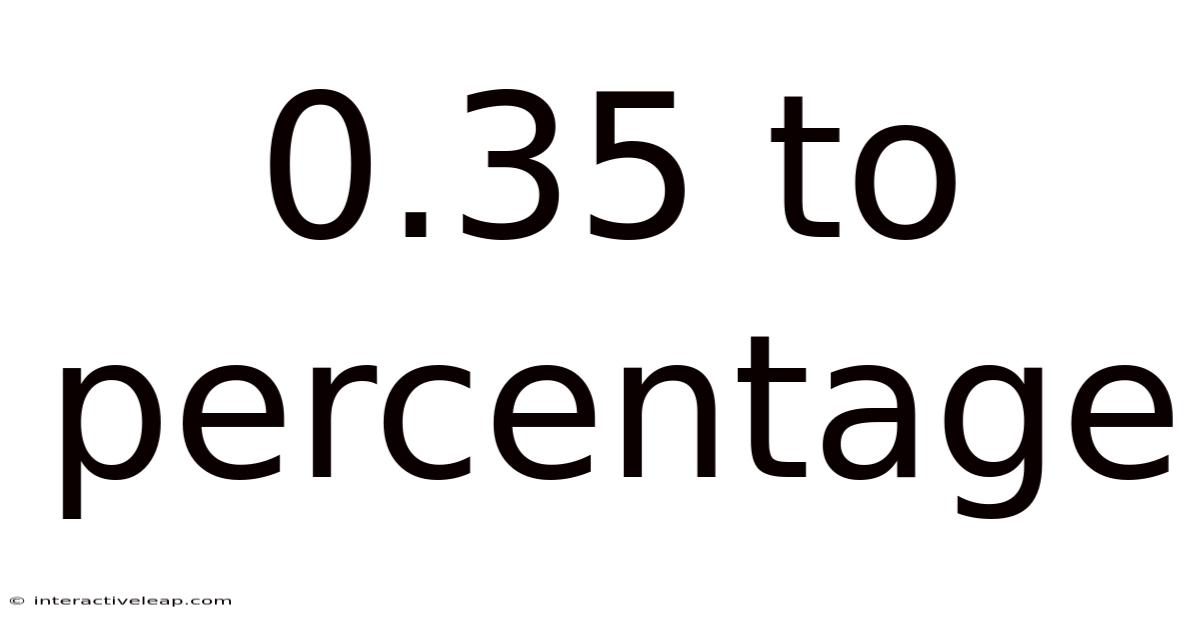
Table of Contents
Converting 0.35 to Percentage: A Comprehensive Guide
Understanding how to convert decimals to percentages is a fundamental skill in mathematics and has wide-ranging applications in various fields, from finance and statistics to everyday calculations. This comprehensive guide will walk you through the process of converting 0.35 to a percentage, explaining the underlying principles and providing practical examples. We'll explore the concept in detail, addressing common questions and misconceptions along the way. By the end, you'll not only know the answer but also understand the why behind the conversion, empowering you to tackle similar problems with confidence.
Understanding Decimals and Percentages
Before diving into the conversion, let's refresh our understanding of decimals and percentages. A decimal is a number that uses a decimal point to separate the whole number part from the fractional part. For example, in the number 0.35, '0' represents the whole number part, and '.35' represents the fractional part, indicating 35 hundredths.
A percentage, denoted by the symbol %, represents a fraction of 100. It essentially expresses a portion of a whole as a number out of 100. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
The Conversion Process: 0.35 to Percentage
Converting a decimal to a percentage is a straightforward process involving multiplication by 100. Here's how it works:
-
Multiply the decimal by 100: To convert 0.35 to a percentage, we multiply it by 100: 0.35 x 100 = 35.
-
Add the percentage symbol: The result, 35, is then followed by the percentage symbol (%) to indicate that it represents a percentage.
Therefore, 0.35 is equal to 35%.
Understanding the "Why" Behind the Multiplication
The reason we multiply by 100 is rooted in the definition of a percentage. A percentage is a fraction out of 100. When we multiply a decimal by 100, we are essentially scaling it up to represent that fraction out of 100. Let's illustrate this with an example:
Imagine you have a test with 100 questions. If you answered 35 questions correctly, your score would be 35 out of 100, or 35/100. To express this as a percentage, you would write it as 35%. The decimal equivalent of 35/100 is 0.35. Thus, multiplying 0.35 by 100 gives us the percentage representation.
Practical Applications of Decimal to Percentage Conversion
The conversion of decimals to percentages is crucial in many real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates frequently involves converting decimals to percentages. For instance, an interest rate of 0.05 is equivalent to 5%.
-
Statistics: Representing data proportions and probabilities often uses percentages. A survey showing 0.65 of respondents agreeing with a particular statement translates to 65% agreement.
-
Science: Expressing experimental results, such as the percentage of successful trials or the concentration of a substance, commonly involves converting decimals.
-
Everyday Life: Calculating tips, sales tax, or discounts in shopping situations uses percentage calculations based on decimal conversions.
Working with Percentages Greater Than 100%
It's important to note that percentages can also be greater than 100%. This occurs when the decimal value is greater than 1. For example:
- 1.50 = 150%
- 2.75 = 275%
These percentages simply represent values exceeding the whole (100%).
Converting Percentages Back to Decimals
The reverse process, converting a percentage back to a decimal, is equally important. To do this, you divide the percentage by 100. For example, to convert 35% back to a decimal:
35% / 100 = 0.35
Common Mistakes and How to Avoid Them
While the conversion process itself is straightforward, some common mistakes can occur:
-
Forgetting the percentage symbol: Always remember to add the % symbol after multiplying by 100.
-
Incorrect placement of the decimal point: Ensure you're multiplying the correct decimal value by 100.
-
Misunderstanding percentages greater than 100%: Remember that percentages can exceed 100%, representing values greater than the whole.
Advanced Applications and Further Exploration
The principles of decimal-to-percentage conversion are fundamental to more complex mathematical concepts. These include:
-
Compound Interest Calculations: Understanding percentages is crucial for calculating compound interest, a widely used concept in finance.
-
Statistical Analysis: Percentages are essential for interpreting statistical data, including probability distributions and confidence intervals.
-
Financial Modeling: Building accurate financial models requires a solid grasp of percentage calculations.
-
Data Visualization: Representing data graphically often involves converting data points (which may be in decimal form) into percentages for easier interpretation.
Frequently Asked Questions (FAQ)
Q: Can I convert fractions to percentages directly without converting to decimals first?
A: Yes, you can. To convert a fraction to a percentage, you first divide the numerator by the denominator, then multiply by 100 and add the percentage sign. For example, 1/4 = 0.25 x 100 = 25%.
Q: What if I have a decimal with more than two places after the decimal point?
A: The process remains the same. Multiply the decimal by 100 and add the percentage symbol. For example, 0.357 x 100 = 35.7%.
Q: Why is understanding percentage conversion important?
A: Understanding percentage conversion is crucial for interpreting data, making financial decisions, understanding scientific results, and solving various everyday problems. It’s a foundational skill for many areas of life.
Q: Are there any online tools or calculators available for this conversion?
A: Yes, many online calculators are readily available to assist with decimal-to-percentage conversions. However, understanding the underlying process is essential for applying this knowledge in diverse situations.
Conclusion
Converting 0.35 to a percentage, resulting in 35%, is a fundamental mathematical operation with far-reaching implications. By understanding the underlying principles and the practical applications of this conversion, you equip yourself with a valuable skill applicable across numerous disciplines. This process is not just about memorizing a formula; it's about understanding the relationship between decimals, fractions, and percentages, leading to a deeper appreciation of mathematical concepts and their real-world applications. Remember to practice consistently, and you’ll master this crucial skill in no time.
Latest Posts
Latest Posts
-
102mm In Inches
Sep 19, 2025
-
1 68 To Feet
Sep 19, 2025
-
100 6f To C
Sep 19, 2025
-
Crossword Clue Gloomy
Sep 19, 2025
-
19 3 4
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 0.35 To Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.