0.35 In Percentage
interactiveleap
Sep 25, 2025 · 5 min read
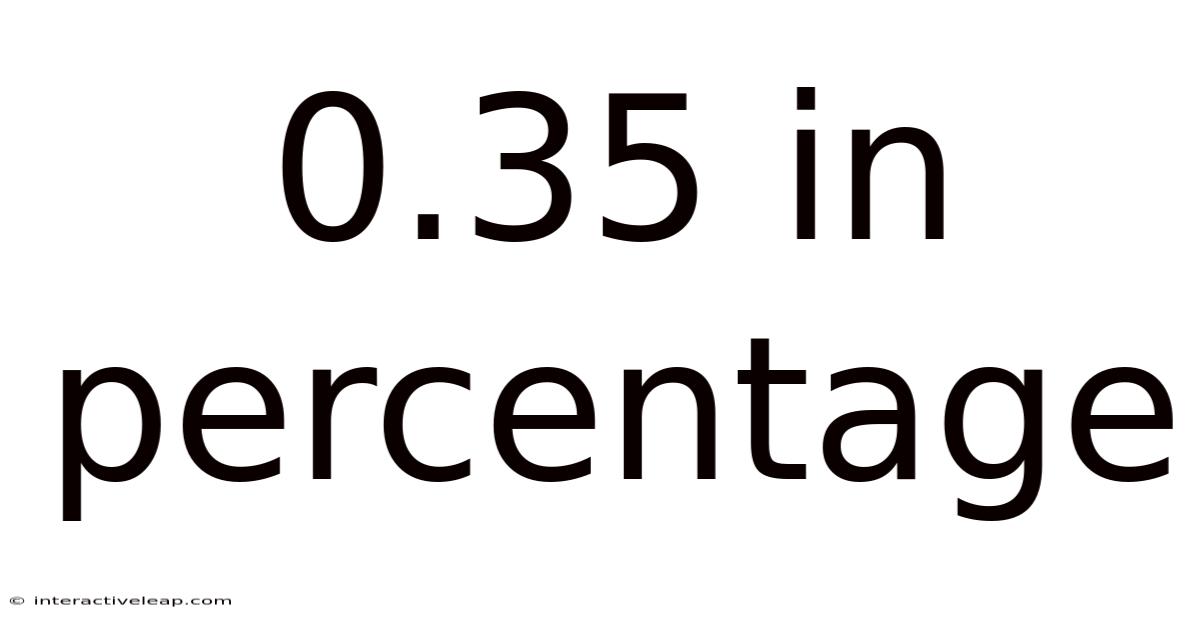
Table of Contents
Decoding 0.35 in Percentage: A Comprehensive Guide
Understanding decimals and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This comprehensive guide will delve into the conversion of 0.35 to a percentage, exploring the underlying principles, providing step-by-step instructions, and offering practical examples to solidify your understanding. We'll also address common misconceptions and answer frequently asked questions, ensuring you gain a robust grasp of this essential concept.
Introduction: Understanding Decimals and Percentages
Before we dive into converting 0.35 to a percentage, let's briefly review the concepts of decimals and percentages. A decimal is a way of representing a number that is not a whole number. It uses a decimal point to separate the whole number part from the fractional part. For example, 0.35 represents 35 hundredths (35/100).
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of a total of 100. For instance, 35% means 35 out of 100, or 35/100. Essentially, percentages are a specific type of fraction expressed as a portion of 100.
Converting 0.35 to a Percentage: A Step-by-Step Guide
The conversion of a decimal to a percentage is a straightforward process. The key is to understand that a percentage is simply a decimal multiplied by 100. Here's a step-by-step guide to convert 0.35 to a percentage:
Step 1: Multiply the decimal by 100
To convert 0.35 to a percentage, we multiply it by 100:
0.35 x 100 = 35
Step 2: Add the percentage symbol (%)
After multiplying by 100, add the percentage symbol (%) to indicate that the result is a percentage:
35%
Therefore, 0.35 is equal to 35%.
Understanding the Underlying Principle: Fractions, Decimals, and Percentages
The relationship between fractions, decimals, and percentages is crucial to grasping the conversion process. Let's explore this relationship using 0.35 as an example:
-
Fraction: The decimal 0.35 can be expressed as a fraction: 35/100. This fraction represents 35 parts out of a total of 100 parts.
-
Decimal: The fraction 35/100 is equivalent to the decimal 0.35. The decimal point separates the whole number part (0) from the fractional part (35).
-
Percentage: To express the fraction 35/100 as a percentage, we multiply the fraction by 100 and add the percentage symbol. This gives us 35%.
Practical Applications of 0.35 (35%)
Understanding the conversion of 0.35 to 35% has numerous practical applications across various fields. Here are a few examples:
-
Sales and Discounts: A store offering a 35% discount means that for every $100 worth of goods, you'll save $35.
-
Taxes: A 35% tax rate indicates that for every $100 of income, $35 will be paid as tax.
-
Statistics and Probability: In statistical analysis, 35% might represent the percentage of respondents who answered a survey question in a particular way.
-
Finance: Financial statements often present data as percentages. For example, a company's profit margin might be 35%, indicating that 35% of its revenue is profit.
-
Science: In scientific experiments, results are often expressed as percentages. For instance, 35% of a sample might exhibit a particular characteristic.
Converting Percentages to Decimals: The Reverse Process
It's equally important to be able to convert percentages back to decimals. The reverse process involves dividing the percentage by 100. For example, to convert 35% back to a decimal:
35% / 100 = 0.35
This demonstrates the reciprocal relationship between decimals and percentages.
Advanced Applications and Further Exploration
The understanding of decimals and percentages extends beyond simple conversions. More complex calculations often involve these concepts. Consider these examples:
-
Calculating percentage increases or decreases: If a value increases from 100 to 135, the percentage increase is calculated as (135-100)/100 * 100% = 35%.
-
Compound interest: Compound interest calculations heavily rely on the application of percentages over multiple periods.
-
Statistical significance: In statistical hypothesis testing, the significance level (often expressed as a percentage) plays a critical role in determining the validity of research findings.
Frequently Asked Questions (FAQs)
Q1: What is the difference between 0.35 and 35%?
A1: While numerically equivalent, they represent different ways of expressing the same value. 0.35 is a decimal, while 35% is a percentage, representing a fraction out of 100.
Q2: How can I convert a fraction to a percentage?
A2: To convert a fraction to a percentage, first convert the fraction to a decimal by dividing the numerator by the denominator. Then, multiply the decimal by 100 and add the percent symbol.
Q3: Can percentages be greater than 100%?
A3: Yes, percentages can be greater than 100%. This represents a value exceeding the original base value. For example, a 150% increase means the value has increased by 50% of its original value.
Q4: Why is understanding percentages important?
A4: Percentages are used extensively in everyday life and across various fields, facilitating comparisons, representing proportions, and making complex data more accessible and understandable.
Q5: Are there any online tools to help with decimal-to-percentage conversions?
A5: Many online calculators and converters are readily available to assist with these conversions. However, understanding the underlying process is crucial for independent problem-solving.
Conclusion: Mastering the Fundamentals
Converting 0.35 to a percentage, while seemingly simple, underpins a critical understanding of mathematical concepts with far-reaching applications. By grasping the relationship between decimals, fractions, and percentages, and practicing the conversion methods, you'll build a strong foundation for tackling more complex mathematical problems and interpreting data effectively in various contexts. Remember, mastering this fundamental skill will empower you to navigate numerical challenges with confidence and accuracy in your personal and professional life. The seemingly straightforward conversion of 0.35 to 35% opens doors to a deeper understanding of quantitative reasoning and its indispensable role in the modern world.
Latest Posts
Latest Posts
-
Crown Neck Tattoo
Sep 25, 2025
-
Stanley Meaning Name
Sep 25, 2025
-
30 Off 140
Sep 25, 2025
-
68 Of 60
Sep 25, 2025
-
Positive Economic Statement
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 0.35 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.