0.3 Of 13850
interactiveleap
Sep 21, 2025 · 5 min read
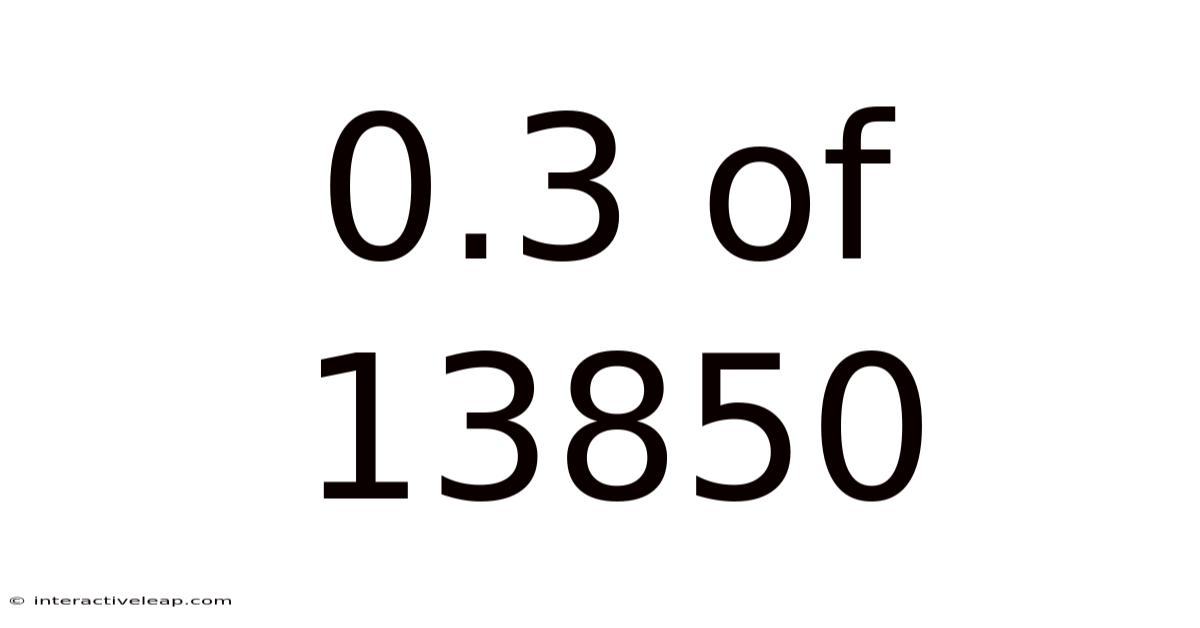
Table of Contents
Decoding 0.3 of 13850: A Deep Dive into Percentages and Their Applications
Finding 0.3 of 13850 might seem like a simple mathematical problem, solvable with a quick calculation. However, understanding the underlying concepts of percentages and their widespread applications unveils a much richer understanding of this seemingly basic calculation. This article delves into the process of calculating 0.3 of 13850, exploring the methodology, providing practical examples, and highlighting the significance of percentage calculations in various fields. We will also explore some common misconceptions and provide a solid foundation for tackling similar problems confidently.
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ( per centum in Latin). It's a universal way to represent proportions and compare different quantities. We use percentages extensively in everyday life, from calculating discounts in shops to understanding financial reports and analyzing statistical data.
The basic formula for calculating a percentage of a number is:
(Percentage/100) * Number = Result
In our case, we want to find 0.3 (or 30%) of 13850. Let's break down the calculation step-by-step.
Calculating 0.3 of 13850: A Step-by-Step Guide
Step 1: Convert the percentage to a decimal.
0.3 is already expressed as a decimal. If the percentage were given as a whole number (e.g., 30%), we would divide it by 100 to get the decimal equivalent (30/100 = 0.3).
Step 2: Multiply the decimal by the number.
Now, we multiply the decimal (0.3) by the number (13850):
0.3 * 13850 = 4155
Therefore, 0.3 of 13850 is 4155.
Practical Applications: Where Percentage Calculations Matter
The ability to calculate percentages is crucial across numerous disciplines. Here are some examples:
-
Finance: Calculating interest on loans or investments, determining tax rates, understanding profit margins, analyzing financial statements, and assessing investment returns all rely heavily on percentage calculations. For example, if a bank offers a 3% interest rate on a savings account with a balance of 13850, the interest earned would be 0.03 * 13850 = 415.5.
-
Retail and Sales: Calculating discounts, markups, sales tax, and profit percentages are essential for businesses. A 30% discount on an item priced at 13850 would reduce the price by 4155, resulting in a final price of 9695.
-
Science and Statistics: Percentages are used extensively in statistical analysis to represent proportions, probabilities, and errors. For example, if a study shows that 30% of a sample population of 13850 individuals exhibit a particular characteristic, then 4155 individuals possess that characteristic.
-
Everyday Life: We encounter percentages daily. Calculating tips in restaurants, understanding sale prices, and determining the percentage of completion of a task are just a few everyday examples where this skill is essential.
-
Education: Percentage calculations are fundamental to grading systems, analyzing test scores, and tracking student performance. For instance, a student scoring 4155 out of 13850 on an exam would achieve a score of approximately 30%.
Beyond the Basics: Advanced Percentage Calculations
While finding 0.3 of 13850 is straightforward, more complex scenarios require a deeper understanding of percentage concepts. Here are some advanced applications:
-
Calculating the Percentage Increase or Decrease: This involves finding the percentage change between two values. The formula is:
((New Value - Old Value) / Old Value) * 100. For instance, if a value increases from 10000 to 13850, the percentage increase is ((13850 - 10000) / 10000) * 100 = 38.5%. -
Finding the Original Value: If you know the result and the percentage, you can work backward to find the original value. For example, if 4155 represents 30% of a value, the original value is 4155 / 0.3 = 13850.
-
Working with Multiple Percentages: Calculations involving multiple percentages often require careful attention to the order of operations. For example, applying a 10% discount followed by a 5% additional discount is not the same as applying a 15% discount.
-
Compounding Percentages: Compounding involves applying a percentage to the result of a previous percentage calculation. This is commonly seen in compound interest calculations.
Addressing Common Misconceptions
Several common misconceptions surround percentage calculations. Let’s clarify some of them:
-
Adding Percentages Directly: You cannot simply add percentages together unless they are applied to the same base value. For example, a 10% increase followed by a 20% increase does not result in a 30% increase.
-
Confusing Percentage Points with Percentages: A change from 10% to 20% is a 10 percentage point increase, not a 100% increase. The percentage increase is actually 100%.
Frequently Asked Questions (FAQ)
Q: What if I need to find a different percentage of 13850?
A: Simply replace 0.3 in the formula with the desired decimal equivalent of the percentage. For example, to find 25% of 13850, you would calculate (0.25 * 13850) = 3462.5.
Q: How can I improve my accuracy in percentage calculations?
A: Practice is key! Work through numerous examples, starting with simple problems and gradually increasing the complexity. Use a calculator to verify your answers and identify areas where you might be making mistakes.
Q: Are there any online tools or calculators available for percentage calculations?
A: Yes, many online calculators are available to perform percentage calculations quickly and accurately. These tools can be very helpful for double-checking your work and speeding up the calculation process. However, understanding the underlying concepts remains crucial.
Conclusion: Mastering the Power of Percentages
Understanding percentages is a fundamental skill with far-reaching applications. While calculating 0.3 of 13850 may seem trivial at first glance, the underlying principles extend far beyond this specific example. Mastering these principles equips you with the tools necessary to tackle more complex problems in finance, statistics, science, and many other fields. Remember to practice regularly, understand the underlying concepts, and utilize tools to enhance your efficiency and accuracy. By doing so, you unlock the power of percentages and their transformative potential in numerous aspects of your life. From understanding financial reports to making informed decisions in everyday life, a strong grasp of percentage calculations provides a significant advantage. The ability to quickly and accurately calculate percentages is a valuable skill that will serve you well throughout your academic and professional pursuits.
Latest Posts
Latest Posts
-
Pint To Milliliter
Sep 21, 2025
-
5 X 17
Sep 21, 2025
-
66 To Feet
Sep 21, 2025
-
66f To Celcius
Sep 21, 2025
-
Meter To Dm
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 0.3 Of 13850 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.