0.04 To Fraction
interactiveleap
Sep 14, 2025 · 5 min read
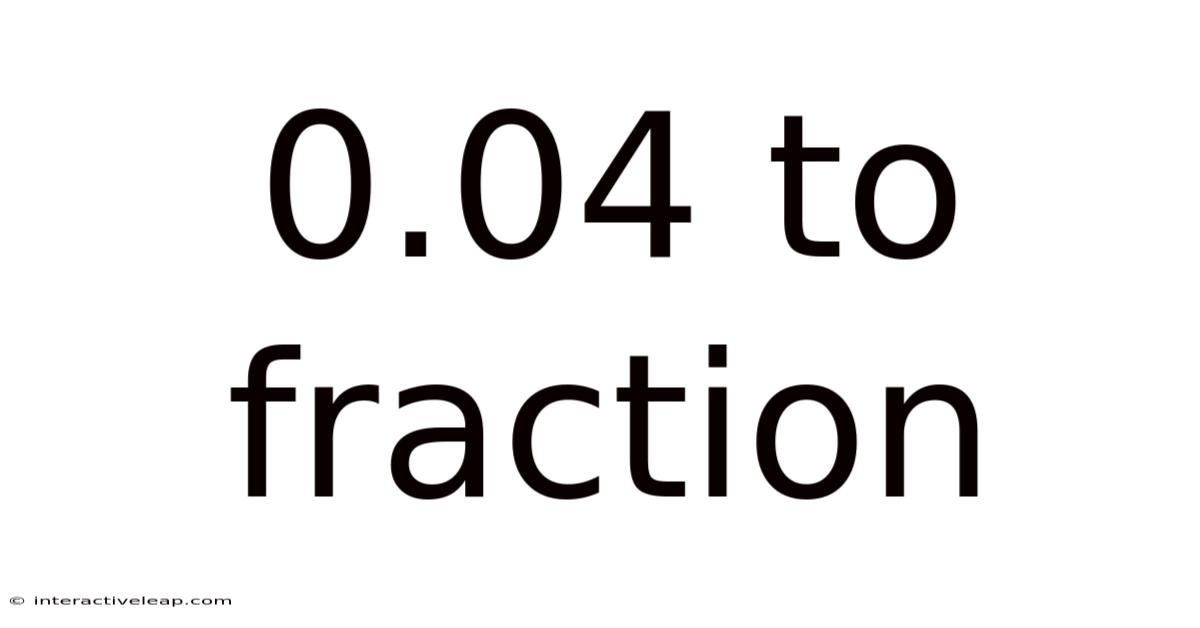
Table of Contents
Converting 0.04 to a Fraction: A Comprehensive Guide
Decimals and fractions are two fundamental ways to represent parts of a whole. Understanding how to convert between them is a crucial skill in mathematics and many related fields. This comprehensive guide will walk you through the process of converting the decimal 0.04 into a fraction, explaining the underlying principles and offering helpful tips for similar conversions. We'll cover the steps involved, the underlying mathematical concepts, frequently asked questions, and even delve into more complex scenarios. By the end, you'll not only know how to convert 0.04 to a fraction but also possess a solid understanding of decimal-to-fraction conversion in general.
Understanding Decimals and Fractions
Before we dive into the conversion process, let's briefly refresh our understanding of decimals and fractions.
A decimal is a way of representing a number that is not a whole number. It uses a decimal point to separate the whole number part from the fractional part. For example, in the decimal 0.04, there are no whole numbers, and 0.04 represents a portion of a whole.
A fraction, on the other hand, represents a part of a whole using a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into. For instance, 1/4 represents one part out of four equal parts.
Steps to Convert 0.04 to a Fraction
Converting 0.04 to a fraction involves a straightforward process:
-
Write the decimal as a fraction with a denominator of 1: This is our starting point. We can write 0.04 as 0.04/1.
-
Remove the decimal point: To do this, we need to multiply both the numerator and denominator by a power of 10. The power of 10 we choose depends on the number of digits after the decimal point. In 0.04, there are two digits after the decimal point, so we multiply by 10<sup>2</sup>, which is 100.
This gives us (0.04 * 100) / (1 * 100) = 4/100.
-
Simplify the fraction: The fraction 4/100 is not in its simplest form. To simplify, we find the greatest common divisor (GCD) of the numerator (4) and the denominator (100). The GCD of 4 and 100 is 4. We divide both the numerator and the denominator by the GCD:
4 ÷ 4 = 1 100 ÷ 4 = 25
This simplifies the fraction to 1/25.
Therefore, 0.04 as a fraction is 1/25.
Mathematical Explanation: Why This Works
The process outlined above works because of the fundamental properties of fractions and decimals. Multiplying both the numerator and denominator of a fraction by the same number (excluding zero) does not change its value. This is because it's essentially multiplying the fraction by 1 (e.g., 100/100 = 1). Multiplying by a power of 10 effectively shifts the decimal point to the right, removing it entirely from the numerator while maintaining the fraction's overall value. Simplifying the fraction ensures we represent the value in its most concise form.
Converting Other Decimals to Fractions
The method used to convert 0.04 to a fraction can be applied to other decimals as well. The key steps remain the same:
- Write the decimal as a fraction over 1.
- Multiply the numerator and denominator by a power of 10 to remove the decimal point. The power of 10 will be 10<sup>n</sup>, where 'n' is the number of digits after the decimal point.
- Simplify the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Examples:
- 0.75: 0.75/1 = 75/100 = 3/4 (GCD is 25)
- 0.6: 0.6/1 = 6/10 = 3/5 (GCD is 2)
- 0.125: 0.125/1 = 125/1000 = 1/8 (GCD is 125)
- 0.333... (repeating decimal): This requires a slightly different approach, often involving algebraic manipulation to solve for the fraction. Repeating decimals cannot always be expressed as simple fractions.
Dealing with Repeating Decimals
Converting repeating decimals to fractions is a bit more involved. Let's take the example of 0.333... (often written as 0. recurring 3).
-
Let x = 0.333...
-
Multiply both sides by 10: 10x = 3.333...
-
Subtract the original equation from the multiplied equation: 10x - x = 3.333... - 0.333... This simplifies to 9x = 3
-
Solve for x: x = 3/9 = 1/3
Thus, the repeating decimal 0.333... is equivalent to the fraction 1/3. This method involves manipulating the equation to eliminate the repeating part.
Frequently Asked Questions (FAQ)
Q: What if the decimal is a whole number with a decimal part?
A: Treat the whole number and the decimal part separately. Convert the decimal part to a fraction and then add the whole number. For example, 2.5 is 2 + 0.5 = 2 + 1/2 = 5/2.
Q: Why is simplifying the fraction important?
A: Simplifying the fraction reduces it to its most concise form. This makes it easier to understand and work with, and it provides the most accurate representation of the decimal value.
Q: Can all decimals be converted to fractions?
A: Yes, terminating decimals (decimals that end) can always be converted to fractions. Repeating decimals can also be converted to fractions, although the process is more complex. However, irrational numbers (like pi or the square root of 2), which have infinite non-repeating decimal expansions, cannot be expressed as simple fractions.
Q: What are some real-world applications of converting decimals to fractions?
A: Converting decimals to fractions is essential in many fields, including:
- Cooking and baking: Recipes often require fractional measurements.
- Construction and engineering: Precise measurements are vital.
- Finance: Calculations involving percentages and proportions frequently require fractions.
- Science: Many scientific formulas and calculations use fractions.
Conclusion
Converting decimals to fractions is a fundamental mathematical skill with broad applications. The process, as demonstrated with the conversion of 0.04 to 1/25, involves writing the decimal as a fraction over 1, removing the decimal point by multiplying by a power of 10, and simplifying the resulting fraction. Understanding this process not only allows for accurate conversions but also deepens your comprehension of the relationship between decimals and fractions, strengthening your overall mathematical foundation. Remember to practice with various decimals to solidify your understanding and build confidence in performing these conversions. The ability to seamlessly transition between decimals and fractions is a valuable tool in various mathematical and real-world applications.
Latest Posts
Latest Posts
-
3500kg In Tonnes
Sep 14, 2025
-
76kgs In Stone
Sep 14, 2025
-
5 3 As Decimal
Sep 14, 2025
-
Books Of Synonyms
Sep 14, 2025
-
45 Of 30
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 0.04 To Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.