0.008 To Fraction
interactiveleap
Sep 22, 2025 · 5 min read
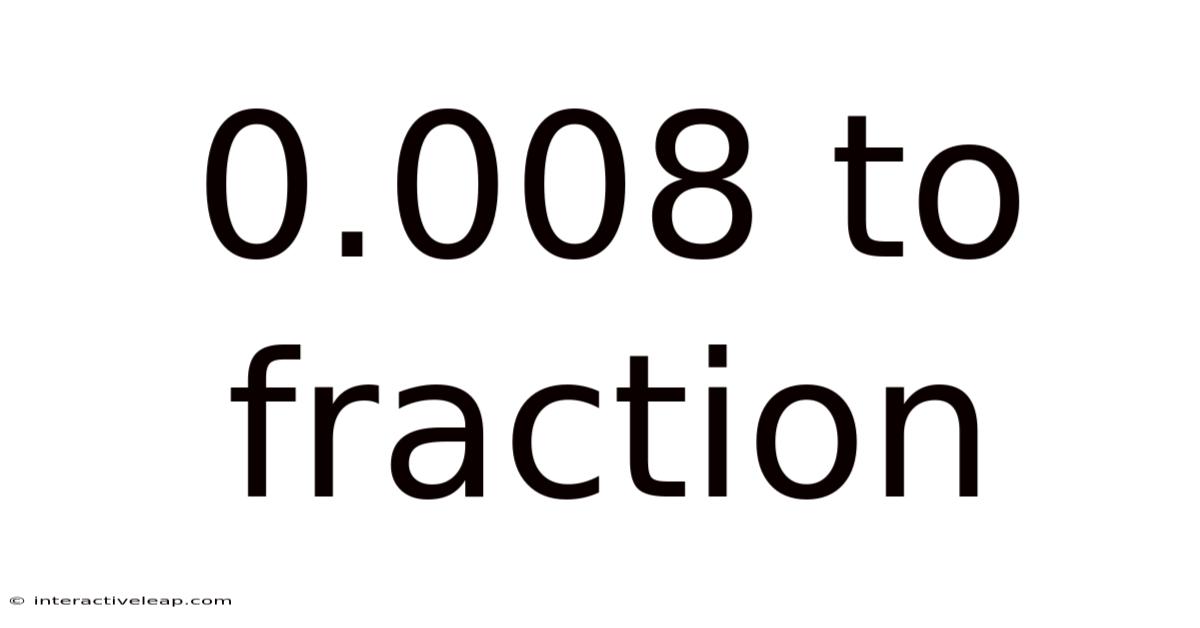
Table of Contents
Converting 0.008 to a Fraction: A Comprehensive Guide
Understanding how to convert decimals to fractions is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the decimal 0.008 into a fraction, explaining the steps in detail and providing further insights into working with decimals and fractions. We'll cover the method, the simplification process, and answer frequently asked questions to ensure a complete understanding of this concept.
Understanding Decimals and Fractions
Before diving into the conversion, let's refresh our understanding of decimals and fractions. A decimal is a number expressed using the base-ten system, where a decimal point separates the whole number part from the fractional part. For example, in the decimal 0.008, there are no whole numbers, and the fractional part represents eight thousandths.
A fraction, on the other hand, represents a part of a whole. It is expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts, and the numerator indicates how many of those parts are being considered. For example, 1/2 represents one out of two equal parts, or one-half.
Converting 0.008 to a Fraction: Step-by-Step Guide
Converting 0.008 to a fraction involves understanding the place value of each digit in the decimal. The digit 8 is in the thousandths place, meaning it represents 8 out of 1000 parts. This directly gives us our fraction:
Step 1: Write the decimal as a fraction with a denominator of 1.
0.008 = 0.008/1
Step 2: Multiply both the numerator and the denominator by 1000 (or a power of 10 to remove the decimal point). The number of zeros in the power of 10 should match the number of digits after the decimal point.
(0.008 x 1000) / (1 x 1000) = 8/1000
Step 3: Simplify the fraction.
This is the crucial step in converting decimals to fractions. We need to find the greatest common divisor (GCD) of the numerator (8) and the denominator (1000) and divide both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
The factors of 8 are 1, 2, 4, and 8. The factors of 1000 are 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, and 1000.
The greatest common divisor of 8 and 1000 is 8. Therefore, we divide both the numerator and the denominator by 8:
8/8 = 1 1000/8 = 125
This simplifies our fraction to:
1/125
Therefore, 0.008 is equal to 1/125.
Scientific Explanation and Mathematical Principles
The process of converting decimals to fractions relies on the fundamental principle of place value in the decimal system. Each digit after the decimal point represents a power of ten in the denominator. For example:
- 0.1 = 1/10 (one-tenth)
- 0.01 = 1/100 (one-hundredth)
- 0.001 = 1/1000 (one-thousandth)
- 0.008 = 8/1000 (eight-thousandths)
Multiplying the decimal by a power of 10 (e.g., 10, 100, 1000) effectively shifts the decimal point to the right, making it a whole number. The same multiplication must be applied to the denominator (which is initially 1) to maintain the equality. The resulting fraction can then be simplified by finding the greatest common divisor of the numerator and the denominator and dividing both by it. This simplification ensures the fraction is expressed in its lowest terms, meaning there is no common factor other than 1 between the numerator and the denominator.
Working with Different Decimals
The method described above can be applied to any decimal number. For example, let's convert 0.25 to a fraction:
- 0.25 = 0.25/1
- (0.25 x 100) / (1 x 100) = 25/100
- Simplifying: GCD(25, 100) = 25. 25/25 = 1; 100/25 = 4. The simplified fraction is 1/4.
Another example: Converting 0.125 to a fraction:
- 0.125 = 0.125/1
- (0.125 x 1000) / (1 x 1000) = 125/1000
- Simplifying: GCD(125, 1000) = 125. 125/125 = 1; 1000/125 = 8. The simplified fraction is 1/8.
Frequently Asked Questions (FAQ)
Q: What if the decimal is a recurring decimal (e.g., 0.333...)?
A: Recurring decimals require a slightly different approach. They cannot be directly converted using the method described above. Special techniques are needed to convert recurring decimals into fractions. This typically involves setting up an equation and solving for the unknown.
Q: How do I know if my fraction is in its simplest form?
A: A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and the denominator is 1. This means there are no common factors (other than 1) that divide both the numerator and the denominator evenly.
Q: What if the decimal has a whole number part (e.g., 2.5)?
A: For decimals with a whole number part, you treat the whole number and the decimal part separately. For example:
- 2.5 can be written as 2 + 0.5
- Convert 0.5 to a fraction: (0.5 x 10) / (1 x 10) = 5/10 = 1/2
- Combine the whole number and the fraction: 2 + 1/2 = 2 1/2 or 5/2 (improper fraction).
Q: Why is simplifying the fraction important?
A: Simplifying a fraction makes it easier to understand and use. It represents the same value in a more concise and manageable form.
Conclusion
Converting decimals to fractions is a fundamental skill with practical applications across various fields. By understanding the principles of place value, greatest common divisors, and the step-by-step process outlined in this guide, you can confidently convert any decimal number to its equivalent fraction. Remember to always simplify the fraction to its lowest terms for the most accurate and efficient representation. This process enhances your mathematical understanding and lays a strong foundation for more advanced mathematical concepts. The ability to seamlessly transition between decimal and fractional representations is essential for success in mathematics and related disciplines.
Latest Posts
Latest Posts
-
1 86 In Ft
Sep 22, 2025
-
Hunger Games Clove
Sep 22, 2025
-
60 Of 270
Sep 22, 2025
-
101 8f To C
Sep 22, 2025
-
52kgs In Lbs
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 0.008 To Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.